Математический конкурс 2016/17 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (Сергей Львовский)
Когда угол между часовой и минутной стрелками больше: в пять минут двенадцатого или в десять минут первого?

Задача 57. (Михаил Евдокимов)
В многодетной семье у каждого ребёнка спросили: «Сколько у тебя братьев?» Каждый из детей назвал одно натуральное число, а сумма всех названных чисел оказалась равна 35. Сколько детей в семье, если все дети ответили правильно?

Задача 58. (Михаил Евдокимов)
Из девяти одинаковых кирпичей-уголков, каждый из которых склеен из трёх кубиков 1x1x1, можно сложить куб 3x3x3 (см. задачу 16 конкурса). Один из кирпичей-уголков потеряли и заменили его прямым кирпичом 3x1x1. Можно ли из нового набора сложить куб 3x3x3?

Задача 59. (Александр Перепечко)
Двое игроков по очереди забирают камешки из большой кучи камней. Первый забирает один камешек, а далее каждый игрок берёт либо на камешек больше, либо на камешек меньше, чем соперник перед ним, но не менее одного камешка. Проигрывает тот, кто не может сделать ход. Кто выиграет при оптимальной игре, если игроки не могут оценить размер кучки, пока в ней больше десяти камешков?

Задача 60. (Андрей Егоров)
С какого-то момента директор компании «Не обманешь – не продашь» стал ежемесячно заявлять собранию акционеров, что доход за последние 7 месяцев превосходит расход, а налоговой инспекции – что расход за последние 12 месяцев превосходит доход. Как долго это может продолжаться, если директор не врёт?

XI тур
Задача 51. (Алексей Канель-Белов)
Известно, что в некотором **84 году количество сред равнялось количеству пятниц. Верно ли, что при этом и число четвергов такое же?

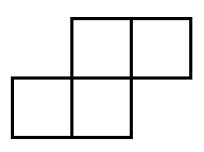
Задача 52. (Александр Толмачёв)
Какое наименьшее количество клеток надо отметить на доске 9х9 так, чтобы среди любых четырёх клеток, образующих фигуру на рисунке, была хотя бы одна отмеченная клетка? (Фигуру можно поворачивать и переворачивать.)

Задача 53.
В стране лжецов и рыцарей (рыцари всегда говорят правду, лжецы всегда лгут) десяти жителям выдали различные числа от 1 до 10. Потом каждого спросили: «Делится ли ваше число на 2?». Утвердительный ответ дали 3 человека. На вопрос «Делится ли ваше число на 4?» утвердительный ответ дали 6 человек. На вопрос «Делится ли ваше число на 5?» утвердительно ответили 2 человека. Сколько было лжецов и какие у них были числа?

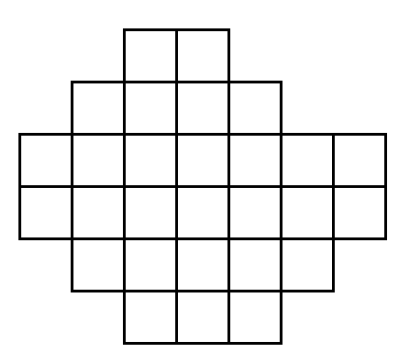
Задача 54. (Михаил Евдокимов)
Разрежьте бумажную клетчатую фигуру на рисунке по линиям сетки на несколько одинаковых, каждая из которых состоит более чем из одной клетки.

Задача 55. (Михаил Евдокимов)
Найдите наибольшее целое число с таким свойством: все его цифры различны, и у числа, в 8 раз большего, тоже все цифры различны.

X тур
Задача 46. (Михаил Евдокимов)
На конференции присутствовали представители двух конкурирующих фирм «Megasoft» и «Gamesoft» Алекс, Бен и Карл. Представители одной и той же компании всегда говорят правду друг другу и врут конкурентам. Алекс сказал Бену: «Карл из Megasoft». Бен ответил: «Я тоже». Где работает Алекс?

Задача 47. (Михаил Евдокимов)
У двух игроков есть кубическая картонная коробка, в которой лежит приз. Они по очереди выбирают одно из рёбер коробки и разрезают коробку вдоль этого ребра. Выигрывает тот, после чьего хода можно открыть коробку и достать приз. Кто может обеспечить себе победу – начинающий или второй игрок? Коробка открывается, если она разрезана вдоль трёх рёбер одной грани.

Задача 48. (Михаил Евдокимов)
Костя приехал в аэропорт, посмотрел на электронное табло, которое показывает время (часы и минуты), и заметил, что на табло горят четыре различные цифры. Когда он посмотрел на табло в следующий раз, там снова горели четыре различные цифры. Какое наименьшее время могло пройти между двумя этими моментами?

Задача 49. (Александр Романов)
Метроморфы могут менять свой рост. Двадцать пять метроморфов стали в одну шеренгу, рост каждого – целое число сантиметров. В конце каждой минуты все метроморфы, слева и справа от которых более низкие, чем они, уменьшают свой рост на 1 см, а те, слева и справа от которых более высокие, увеличивают свой рост на 1 см. Остальные, в том числе и стоящие по краям шеренги, не меняют роста. а) Докажите, что через несколько минут все метроморфы перестанут менять свой рост. б) Верно ли это утверждение, если метроморфы уменьшают и увеличивают свой рост на 2 см?

Задача 50. (Валерий Сендеров, Борис Каневский)
а) Дан клетчатый квадрат 15x15. Можно ли закрасить 15 клеток так, чтобы любой прямоугольник 3x5 со сторонами, параллельными сторонам квадрата, составленный из клеток, содержал хоть одну закрашенную клетку? б) А можно ли так закрасить всего 14 клеток?

IX тур
Задача 41. (Сергей Дворянинов)
В последнюю среду января я приехал в Приэльбрусье кататься на лыжах, но в последний вторник января погода испортилась и, как оказалось, надолго. Поэтому во второй четверг февраля я уехал домой. Какого числа я уехал домой и сколько дней я провёл в горах?

Задача 42. (Алексей Канель-Белов)
Население города Тмутаракань состоит из прусаков и кукарач, всего не более 2000000 жителей. Каждый прусак знаком с 1000 кукарачами, а каждая кукарача – с 1001 прусаком. Знакомство взаимное. Каково максимальное число обитателей города?

Задача 43. (Егор Бакаев)
Дан квадрат 6x6 (см. рисунок). Одним действием можно выбрать какую-нибудь строку или столбец и перекрасить каждую из 6 клеток в противоположный цвет. Можно ли с помощью нескольких таких действий получить исходную картинку, повёрнутую на 180°?


Задача 44. (Михаил Евдокимов)
Вася и девять его друзей живут на берегу круглого озера в 10 домах, расположенных через каждые 100 метров по периметру (см. рисунок). Однажды Вася решил собрать друзей вместе. Он выбирает дом, где ещё не был, идёт туда и забирает друга с собой, потом выбирает следующий дом, и т.д. Между двумя домами Вася всегда идёт по кратчайшему маршруту, но очерёдность посещения может быть произвольной. Какое наибольшее расстояние мог пройти Вася к моменту, когда все они собрались дома у последнего из друзей?


Задача 45. (Александр Грибалко)
На учительском столе были выставлены в ряд внешне одинаковые гирьки массой 101 г, 102 г, …, 110 г (именно в таком порядке). На перемене Вовочка поменял местами две соседние гирьки. Учителю это известно. Как ему за два взвешивания на чашечных весах определить, какие именно гирьки были переставлены?

VIII тур
Задача 36. (М. Варга)
Каждый номер журнала «Квантик» состоит из обложки и восьми двойных листов: они вкладываются друг в друга и соединяются скобами. На каком из восьми листов сумма номеров всех четырёх страниц листа самая большая?

Задача 37. (Дмитрий Баранов)
Ноутик записал на доске три числа: 1/9, 1/10 и 1/11. Квантик за ход называет любое число, а Ноутик увеличивает ровно одно из чисел на доске на число, названное Квантиком. Может ли Квантик делать ходы так, чтобы обязательно в какой-то момент хоть одно из трёх чисел на доске превратилось в 1?

Задача 38. (Михаил Евдокимов)
Фигуру, изображённую на рисунке, разрежьте по линиям сетки на две одинаковые части, из которых можно сложить квадрат 6x6 (части разрешается переворачивать).

Задача 39. (Алексей Канель-Белов)
В волшебном дворце обитают прекрасные феи. Каждый день у всех фей, кроме одной, улучшаeтся и обаятельность, и привлекательность, а у оставшейся феи – только одно из этих качеств (а другое может и ухудшиться). Однако за последний год все феи совершенно не изменились. Каково наибольшее возможное число фей во дворце? (В году 365 дней.)

Задача 40. (Сергей Дворянинов)
Из круга можно вырезать четырёхугольник, у которого две противоположные стороны равны а и с, а две другие – b и d. Толик Втулкин утверждает, что тогда из этого круга можно вырезать и четырёхугольник, у которого две противоположные стороны равны a и b, а две другие – c и d. Прав ли Толик? Решите задачу в случаях, когда исходный четырёхугольник
а) вписан в данный круг (вершины четырёхугольника лежат на границе круга);
б) не обязательно вписан, но выпуклый (диагонали лежат внутри четырёхугольника);
в) может быть невыпуклым (одна из диагоналей может лежать снаружи четырёхугольника).

VII тур
Задача 31. (Михаил Евдокимов)
Барон Мюнхгаузен утверждает, что когда он обходит снаружи свой замок вдоль его стен и возвращается в исходную точку, то проходит больше 800 метров, а когда он идёт вдоль забора, которым обнесён замок, и возвращается в исходную точку, то проходит меньше 400 метров. Могут ли слова барона быть правдой?

Задача 32. (Михаил Евдокимов)
Вы наверняка знаете, что таблица 3x3, заполненная целыми числами от 1 до 9 так, что суммы чисел в каждой строке, каждом столбце и на обеих диагоналях одинаковы, называется магическим квадратом 3x3 (см. пример на рисунке).
а) Подберите 9 различных целых чисел и заполните ими таблицу 3x3 так, чтобы произведения чисел в каждой строке, каждом столбце и на обеих диагоналях были одинаковы.
б) Можно ли подобрать эти различные целые числа в предыдущем пункте так, чтобы среди них были 15 и 25?

Задача 33. (Елена Коннова)
Квантик и Ноутик играют в необычный морской бой. Ноутик составил из восьми кораб лей 1x3 и одного корабля 1x1 квадрат 5x5 клеток (корабли стоят вплотную друг к другу). За ход Квантик делает выстрел в одну из клеток, а Ноутик сообщает, в какой корабль Квантик попал и какие клетки квадрата занимает этот корабль. Цель Квантика – поразить корабль 1x1. За какое наименьшее число выстрелов он может гарантированно этого добиться?

Задача 34. (Григорий Гальперин)
Есть 12 карточек, на каждой написана одна ненулевая цифра. Известно, что из этих карточек можно составить два шестизначных числа, сумма которых равна 1099999. Докажите, что из этих карточек можно составить два шестизначных числа, сумма которых равна одному миллиону.

Задача 35.
Имеются восемь монет, семь из которых одинаковые, а одна фальшивая и отличается по весу (неизвестно, в какую сторону). Также имеются чашечные весы, которые показывают правильный результат, если на чашах разный вес, а если вес одинаковый, то вместо равенства показывают что попало.
а) Придумайте способ найти фальшивую монету и узнать, тяжелее она настоящих или легче.
б) Можно ли гарантированно найти фальшивую монету всего за 4 взвешивания?

VI тур
Задача 26. (Егор Бакаев)
Разрежьте фигурку на рисунке на три части, равные по площади и периметру.

Задача 27. (Егор Бакаев)
По кругу сидело 10 болтунов. Сначала один из них рассказал один анекдот, следующий по часовой стрелке – два анекдота, следующий – три, и так далее по кругу, пока один не рассказал 100 анекдотов за раз. Тут болтуны устали, и следующий по часовой стрелке рассказал 99 анекдотов, следующий – 98, и так далее по кругу, пока один не рассказал всего один анекдот, и все разошлись. Сколько всего анекдотов рассказал каждый из этих 10 болтунов?

Задача 28. (Николай Авилов)
На каждой стороне квадрата отметили по три точки, отличные от его вершин. От каждой точки внутрь квадрата отложили по отрезку, перпендикулярному соответствующей стороне квадрата. Могло ли случиться, что каждый отрезок пересёк (под прямым углом) ровно а) 4 других отрезка; б) 5 других отрезков?

Задача 29. (Михаил Евдокимов)
Все 36 карт колоды выложены рубашкой вверх в виде «квадрата» 6x6, как показано на рисунке. За один вопрос игрок может выбрать 9 карт, образующих «квадрат» 3x3, и узнать набор карт, который им соответствует (без указания места, где какая карта лежит).
а) Докажите, что за несколько вопросов игрок может определить любую карту, на которую укажет ведущий.
б) Какое наименьшее число вопросов достаточно, чтобы узнать угловую карту?

Задача 30. (Михаил Евдокимов)
На стороне BC квадрата ABCD взяли точку M так, что BM в три раза длиннее MC. Докажите, что окружность, описанная около треугольника ABM, касается одной из сторон квадрата ABCD.

V тур
Задача 21.
Два поезда едут навстречу друг другу: один со скоростью 20 км/ч, его длина 600 м, а второй со скоростью 40 км/ч, его длина 400 м. Машинисты поездов встретились в полдень. Когда встретились кондукторы, едущие в хвостах этих поездов?

Задача 22. (Павел Кожевников)
а) Найдутся ли 3 целых числа, которые все различны и куб каждого из них делится на произведение остальных чисел?\n б) А найдутся ли 4 таких числа?

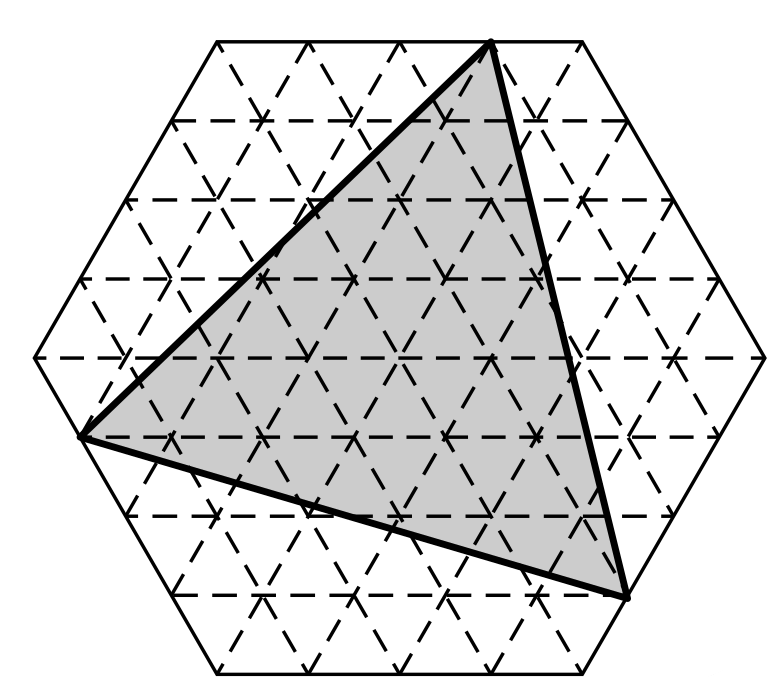
Задача 23. (Степан Кузнецов)
Шестиугольник на рисунке составлен из 96 одинаковых равносторонних треугольников площади 1. Найдите площадь серого треугольника.
Задача 24.
Докажите, что количество всех цифр в последовательности 1, 2, 3, 4, … , 1000 равно количеству всех нулей в последовательности 1, 2, 3, 4, … , 10000.

Задача 25. (Лев Емельянов)
а) Куб 3x3x3 сложен из 27 синих кубиков (26 мы видим, а один находится внутри). Имеются также синяя и белая краски. За ход разрешается выбрать любой видимый кубик и перекрасить его, а также все кубики, имеющие с выбранным общую грань, по правилу: синий – в белый, белый – в синий (на рисунке приведён пример хода, когда был выбран угловой кубик). Сделайте несколько ходов так, чтобы получился куб, белый снаружи.
б)* Рассмотрим все возможные варианты окраски 26 видимых кубиков в синий и белый цвета (каждый кубик красится целиком в один из цветов). Каждый ли из этих вариантов можно получить из синего куба за несколько ходов?

IV тур
Задача 16. (Михаил Евдокимов)
Можно ли из одинаковых кирпичей-уголков, каждый из которых склеен из трёх кубиков 1x1x1, сложить куб 3x3x3?


Задача 17. (Егор Бакаев)
Ради равноправия полов учитель, когда ставит пятёрку девочке, ставит пятёрку и какому-нибудь мальчику. А когда ставит пятёрку мальчику, ставит пятёрку ещё какой-нибудь девочке. Также ради справедливости учитель хочет, чтобы к концу года у всех детей было поровну пятёрок. Получится ли у него этого добиться, если в классе 23 ребёнка, и хотя бы одну пятёрку за год он всё-таки хочет поставить?

Задача 18. (Егор Бакаев)
На каждой из 6 карточек написана цифра от 1 до 6 (каждая по одному разу). На листке написана «заготовка» арифметического выражения:
(* + )·( + )·( + *).
Петя выбирает одну из звёздочек и кладёт на неё одну из карточек, затем то же самое делает Вася, затем снова Петя, и так далее поочереди. Вася хочет, чтобы, когда все карточки будут выложены, результат выражения равнялся 240. Сможет ли Петя ему помешать?

Задача 19. (Михаил Евдокимов)
Можно ли круглую монету диаметра 2 см положить на лист клетчатой бумаги (сторона клетки 0,5 см) так, чтобы она покрыла ровно 10 узлов сетки? (Узел, попавший на границу монеты, тоже считается покрытым.)

Задача 20. (Сергей Костин)
В лифте 16-этажного дома работают только две кнопки. При нажатии на первую кнопку лифт поднимается на 5 этажей, а при нажатии на вторую опускается на 7 этажей (если это невозможно, лифт никуда не едет). Человек зашёл в лифт на первом этаже. На каком этаже он может оказаться после 99 переездов лифта? (Найдите все варианты и докажите, что других нет.)

III тур
Задача 11.
Напишите десять чисел так, чтобы каждое следующее число было не меньше предыдущего, сумма их квадратов равнялась 2, и третье по счёту число было как можно больше.
Задача 12.
Разрежьте треугольник на четыре треугольные части так, чтобы любые две из них прилегали друг к другу, то есть имели общий отрезок границы.

Задача 13. (Михаил Евдокимов)
Четыре логика A, B, C и D сидят за круглым столом в этом порядке (если двигаться по часовой стрелке). Им показали девять карт одной масти (шестёрка, семёрка, …, король, туз), а потом перемешали и выдали по карте, так что каждый видит лишь свою карту. Логикам по очереди задали один и тот же вопрос: «Ваша карта старше, чем у вашего соседа справа?» Логик А ответил «не знаю». Услышав его ответ, Б тоже ответил «не знаю». Тогда и С ответил «не знаю», а вслед за ним и D дал такой же ответ. Какая карта у D? (Когда логик отвечает «не знаю», это означает, что и ответ «да», и ответ «нет» могли бы оказаться неверными.)

Задача 14.
а) Куб перекатывают по плоскости, поворачивая его вокруг рёбер (без проскальзывания). После нескольких перекатываний куб вернулся на прежнее место (поверх того же квадрата, который был под ним изначально). Обязательно ли каждая вершина куба оказалась там, где была вначале (не попала в другую вершину квадрата)?
б) Аналогичный вопрос для правильного тетраэдра (все четыре грани – равносторонние треугольники).

Задача 15.
а) У каждого из 12 пиратов есть некоторое количество золотого песка. Они могут встречаться по двое или по трое; при встрече весь имеющийся у участников встречи песок делится поровну. Докажите, что пираты могут добиться, чтобы после нескольких встреч у всех было поровну песка.
б) Верно ли аналогичное утверждение для 13 человек, если разрешается встречаться в любом составе, только не всем вместе, и делить песок поровну?

II тур
Задача 6.
Семеро девочек стоят в ряд, как показано на рисунке, и держат в руках конфеты. У девочек, которых вы видите справа от Тани – 13 конфет, справа от Ксюши – 33, справа от Ани – 23, справа от Иры – 8, справа от Вали – 27, справа от Нади – 16. Сколько конфет у Кати?

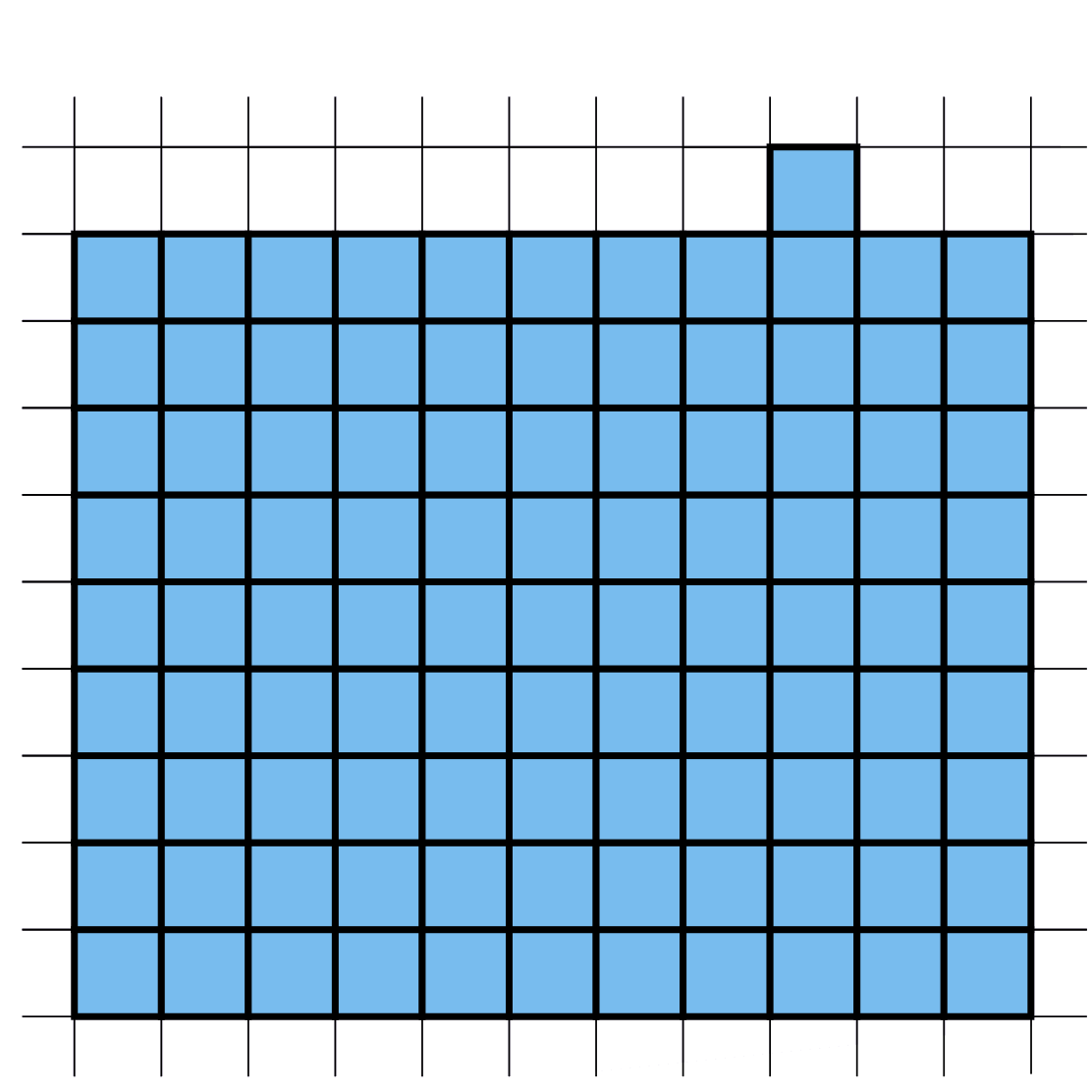
Задача 7. (Егор Бакаев)
Разрежьте синюю фигуру, изображённую на рисунке, на 10 равных частей.
Задача 8. (Ольга Зайцева-Иврии)
Можно ли разложить несколько яблок по 10 тарелкам так, чтобы на любых двух тарелках было вместе либо 5, либо 8, либо 11 яблок и все три варианта встречались? Если да, то сколько всего могло быть яблок? Укажите все возможности.

Задача 9.
Вася знает, что если в треугольнике провести три средние линии, то получатся четыре одинаковых треугольника. Он решил, что если в тетраэдре (треугольной пирамиде) провести через середины рёбер четыре «средние плоскости», то получатся пять одинаковых тетраэдров поменьше. А что получится на самом деле? Сколько вершин и граней будет у этих многогранников?

Задача 10.
Трое рабочих вырыли яму. Они работали по очереди, причём каждый проработал столько времени, сколько нужно было бы двум другим, чтобы вместе вырыть половину ямы. Во сколько раз быстрее они вырыли бы яму, работая все вместе?

I тур
Задача 1.
Две гоночные машины — красная и зелёная — выехали из города А в город Б по одной и той же дороге, стартовав и финишировав одновременно. При этом зелёная машина ни разу не обгоняла красную. Могло ли быть так, что не менее 90% времени зелёная машина ехала быстрее красной?

Задача 2.
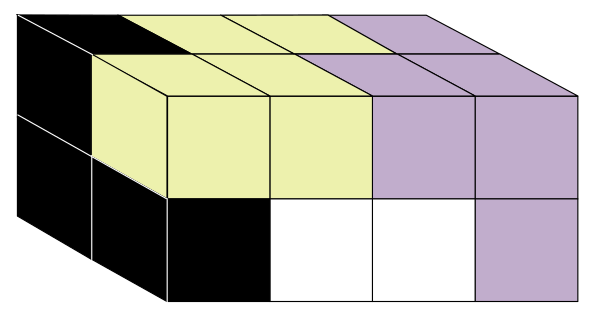
Имеются 4 детали, каждая склеена из четырёх кубиков и окрашена в свой цвет. Из них сложили кирпич размером 2x2x4 без дырок (см. рисунок). Как выглядит белая деталь?

Задача 3. (Михаил Евдокимов)
Квантик по-разному расставлял скобки в выражении a—b—c—d, где a, b, c, d — некоторые числа (не обязательно целые). Могли ли в зависимости от расстановки скобок получиться и 1, и 2, и 3, и 4?

Задача 4. (Игорь Рубанов)
На клетчатой бумаге нарисовали квадрат 5x5, разделённый на 25 квадратиков 1x1. Можно ли выбрать 16 квадратиков и провести в каждом одну диагональ так, чтобы никакие две диагонали не имели общего конца?

Задача 5.
Путешественник приехал в гостиницу утром, имея при себе 37 золотых монет. Хозяин объясняет ему правила: «Каждый вечер ты должен отдавать мне в уплату за прошедший день одну или больше монет, сколько захочешь. Но если за какой-то период (один или несколько подряд идущих дней) ты мне заплатишь ровно 7 монет, то больше оставаться нельзя». Удивился путешественник и стал прикидывать, какое наибольшее число дней он может провести в гостинице по таким правилам. Что это за число? Как может действовать путешественник? Почему нельзя прожить больше?


