
Our mathematical competition for the 2020/2021 academic year has started! It is held in three stages: from September to December, from January to April and from May to August. Diplomas and prizes will be awarded to the winners of the entire year as well as to the winners of each stage. We invite everyone to join!
Please send your solutions to matkonkurs@kvantik.com.
Good luck!
Tour III
Задача 11. (Grigory Galperin)
a) Is it possible to make up a 1001-digit number from non-zero digits with the following property: if you cross out several digits in it (not necessarily in a row) so that a seven-digit number remains, then this remaining number will not be divisible by 77?
The same question for the following property: if you cross out several digits in it (not necessarily in a row) so that a six-digit number remains, then this remaining number will not be divisible by 77.

Задача 12.
During one day of stay at the Magic School, the amount of a student’s knowledge increases (relative to the previous day) by a percentage equal to the day of the month. For example, on October 31, knowledge will increase by 31%, and on November 1 only by 1%. Dunno studied at the Magic School for 11 days, from October 10 to October 20, and Doono also studied for 11 days, from October 11 to October 21. Who has more knowledge now and by what percentage, if their knowledge was equal before the Magic School?

Задача 13. (Alexander Perepechko)
Three bird-watchers, each on its own tower, watch over one heron. Bird-watchers look directly at the heron all the time and turn after it. In the morning, the heron flew out of the nest for a hunt and came back in the evening. Is it possible that, as a result, the first bird-watcher made exactly one turn around himself clockwise, the second did exactly one turn counterclockwise, and the third did not make a single full turn at all?

Задача 14. (Mikhail Evdokimov)
Is it possible to write a natural number at each vertex of a cube so that all 8 numbers are different, but the product of the numbers at the vertices of each face is the same?

Задача 15. (Михаил Евдокимов)
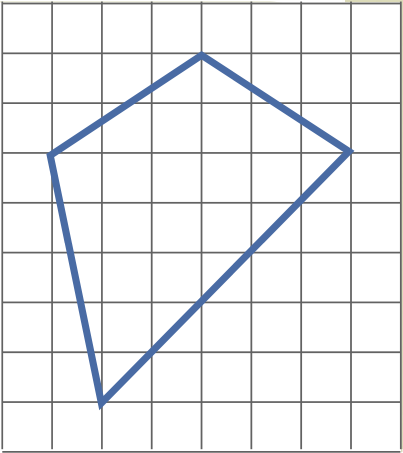
а) A quadrilateral with vertices at the nodes of the grid was drawn on a checkered sheet (see figure). Prove that one of its angles is twice as large as some other.
b) Draw a convex quadrilateral on the checkered sheet with vertices at the nodes of the grid such that one angle of the quadrilateral is four times as large as some other.

Tour II
Задача 6. (Sergey Kostin)
In the spring of a given year, there were fewer Mondays than Thursdays. Which day of week, Tuesday or Friday, was in fewer numbers in the summer of the same year?

Задача 7. (Grigory Galperin)
Find all natural numbers n such that n2 = n! + n. (Reminder: n! denotes the product 1 · 2 · … · n of the first n natural numbers.)

Задача 8. (Danila Ivanov)
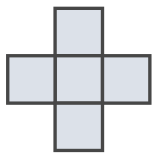
Two players play Tic-Tac-Toe on an infinite checkered plane. The player who marks a cross of five cells (see the picture) wins. Can the second player always prevent the first one from winning?

Задача 9. (Mikhail Evdokimov)
a) Is it possible to color all natural numbers in three colors so that each color is present and the product of any same colored pair of numbers has the same color?
b) Is it possible to do this with seven colors?

Задача 10.
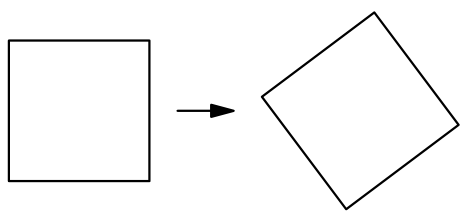
Figure out a way to cut the square into pieces and translate them without rotating or flipping so that you get an equal, but rotated square (for example, as in the picture).

Tour I
Задача 1. (Gregory Galperin)
Gregory has put three weights of 1/8, 1/9, and 1/10 grams on the left side of pan scales. Is it possible to put two weights equal to rational fractions with numerator 1 to the right side so that they would balance the left side of the scales?

Задача 2. (Alexander Perepechko)
There are three houses on a circle at equal distances from each other. Which way from one house to another is the shortest: along the arc of a circle (blue line) or through the center of the circle (green line)?

Задача 3. (Nikolay Avilov)
Numbers that correspond to the dates of each month are indicated on the sheets of a 1-year tear-off calendar. A playful boy Peter wants to tear off a few sheets (not necessarily consecutive) so that the remaining sheets would contain no two numbers such that one them is three times larger than the other. What is the smallest number of sheets he has to tear off?

Задача 4. (Egor Bakaev)
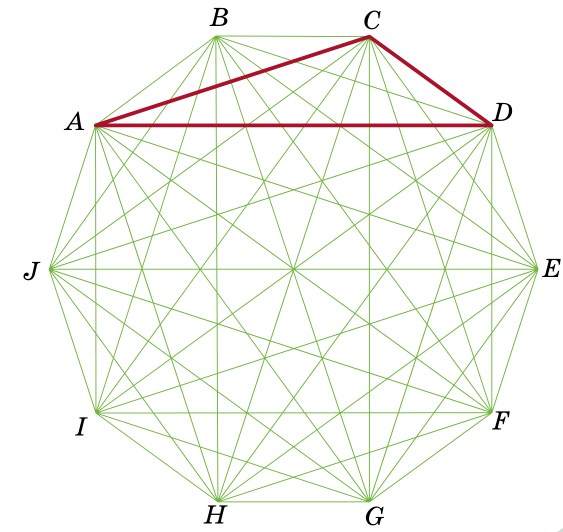
Given a regular decagon ABCDEFGHIJ (all sides are equal, all angles are equal), what part of its area does the triangle ACD take up?

Задача 5. (Pavel Kozhevnikov)
There is a rectangle on the checkered plane (all cells are squares 1 × 1) drawn along grid lines. The rectangle was cut into N rectangles along the grid lines by several horizontal and vertical cuts from one side to the other. Prove that it is possible to paint some of these N rectangles (maybe only one or all) so that the colored area would be a rectangle of area divisible by N.


