Задача 46.

Вадик и Саша увидели старые весы (со стрелкой) и взвесили на них свои портфели. Весы показали 5 кг и 4 кг. Когда они взвесили оба портфеля вместе, весы показали 8 кг.
– Как же так? – воскликнул Саша. – Пять плюс четыре не равняется восьми!
– Разве ты не видишь? – ответил Вадик. – У весов сдвинута стрелка. Так сколько же весили портфели на самом деле?

Задача 47.

Внутри круга отметили точку. Разрежьте круг на две части так, чтобы из них можно было составить новый круг, у которого отмеченная точка будет в центре.

Задача 48.

Автомобильные покрышки стираются на передних колёсах через 25000 км пути, а на задних – через 15000 км пути. Какое наибольшее расстояние удастся проехать на таком автомобиле, если в пути можно поменять покрышки местами?

Задача 49.

Разрешается переставить цифры 1, 3, 4 и 6 в любом порядке и расставить между какими угодно из них знаки арифметических действий +, –, ·, : и скобки (например, так: (63 + 1) : 4). Получите выражение, значение которого равняется 24.

Задача 50.

Среди 10 человек, подозреваемых в преступлении, двое виновных и восемь невиновных. Экстрасенсу предъявляют подозреваемых по трое. Если среди троих есть преступник, экстрасенс указывает на него, если там два преступника – на одного из них, а если преступников нет – на любого из троих.
а) Как за 4 таких сеанса найти хотя бы одного преступника?
б) Как за 6 таких сеансов наверняка выявить обоих преступников?

Задача 41.

Какая цифра встречается реже всего при записи первых ста натуральных чисел? А какая — чаще всего?

Задача 42.

У хозяйки было два клетчатых коврика: 6×6 клеток и 8×8 клеток. Она решила сделать из них один коврик 10×10 клеток. Может ли она добиться этого, разрезав каждый коврик не более чем на две части и не повредив ни одной клеточки?

Задача 43.

Три спортсмена стартовали одновременно из одной точки круговой дорожки. Через некоторое время они вновь одновременно оказались в точке старта. Известно, что за это время самый быстрый спортс­мен обгонял самого медленного 23 раза (обгон в момент старта не учитываем). Сколько всего за это время было случаев, когда один из спортсменов обгонял другого? Спортсмены бегут равномерно, с различными скоростями.

Задача 44.

Дан прямоугольник ABCD. Проведена прямая, которая отсекает от стороны AB одну треть, а от стороны AD — одну четверть, считая от вершины A. Какую часть эта прямая отсекает от диагонали AC?

Задача 45.

а) На столе лежат две кучки по 20 спичек в каждой. Петя и Вася играют в такую игру. Первым ходом Петя перекладывает одну спичку из какой-то кучки в другую, затем Вася тоже перекладывает одну спичку из какой-то кучки в другую. Вторым ходом Петя, а потом Вася, перекладывают уже по две спички, третьим ходом — по три, и так далее. Побеждает тот, после хода которого либо все спички впервые окажутся в одной кучке, либо соперник не сможет сделать свой ход. Придумайте для одного из игроков стратегию — как ему играть, чтобы всегда выигрывать (при любой игре его соперника).
б) Та же задача, но изначально в кучках по 25 спичек.

Задача 36.

Андрей с папой пошли в тир. Уговор был такой: Андрей делает 5 выстрелов и за каждое попадание получает право ещё на 2 выстрела. Всего Андрей выстрелил 25 раз. Сколько раз он попал?

Задача 37.

Прямоугольник ABCD разбит двумя прямыми, пересекающимися в точке X, на 4 прямоугольника (как показано на рисунке).
а) Докажите, что если X лежит на диагонали AC, то площади левого верхнего и правого нижнего прямоугольников равны (на рисунке они закрашены).
б) Пусть известно, что площади левого верхнего и правого нижнего прямоугольников равны. Обязательно ли тогда точка Х лежит на диагонали АС?

Задача 38.

Кассир считает бумажные деньги так: сначала считает, сколько всего купюр (независимо от их достоинства), потом прибавляет число купюр достоинством больше рубля, затем прибавляет число купюр достоинством больше двух рублей, и так далее. Почему у него получается правильный ответ?

Задача 39.

Обезьяна хочет определить, с какого самого низкого этажа 20-этажного дома нужно бросить кокосовый орех, чтобы он разбился. У неё есть два одинаковых ореха. Хватит ли ей для этого шести бросков? (Неразбившийся орех можно бросать снова.)

Задача 40.

Двое играют в игру на белой доске 10×10 клеток. Первый каждым ходом закрашивает чёрным цветом любые 4 белые клетки, образующие квадратик 2×2. Второй каждым ходом закрашивает чёрным цветом любые 3 белые клетки, образующие «уголок». Ходят по очереди, а проигрывает тот, кто не может сделать ход. Кто из игроков может играть так, чтобы всегда выигрывать, как бы ни играл его соперник?

Задача 31.

Заяц соревновался с черепахой в беге на 100 метров. Когда заяц прибежал к финишу, черепахе оставалось пробежать ещё 90 метров. На сколько метров надо отодвинуть назад стартовую линию для зайца, чтобы при новой попытке оба бегуна пришли к финишу одновременно?

Задача 32.

Один странный мальчик по средам и пятницам говорит только правду, по вторникам всегда лжёт, а в остальные дни может и солгать, и сказать правду. Семь дней подряд мальчика спрашивали, как его зовут. Первые шесть ответов, по порядку, были таковы: Женя, Боря, Вася, Вася, Петя, Боря. А как он ответил на седьмой день?

Задача 33.

Как повесить шторы на карниз аккуратно? Вначале вешаем на крайние крючки края шторы. Потом, оттягивая штору, находим её середину и вешаем на средний крючок. То же самое проделываем с каждой половиной, и так далее. При каком числе крючков на карнизе удастся повесить шторы по такому методу? (Дайте простое описание таких чисел.)

Задача 34.

Можно ли нарисовать на листе бумаги четыре равных квадрата и две перпендикулярные прямые так, чтобы квадраты не перекрывались (даже не касались) и каждая прямая пересекала каждый квадрат по отрезку?

Задача 35.

а) В гостиницу на неделю приехал путешественник. У него вместо денег нашлась лишь серебряная цепочка из 7 звеньев, как на рисунке. Хозяин требует платить по одному звену в день без задержек, готов давать сдачу ранее полученными кусками цепочки, но вперёд плату не берёт. Путешественник распилил на цепочке всего одно звено так, что ему удалось расплачиваться все 7 дней. Как он это сделал?
б) В следующий раз у путешественника оказалась цепочка из 23 звеньев. Можно ли распилить всего два звена, чтобы расплачиваться потом ежедневно 23 дня?

Задача 26.

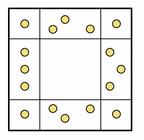
Вдоль стен квадратного бастиона требовалось расставить 16 часовых. Комендант расставил их по 5 человек на стену, как на рисунке. Затем пришел полковник и велел расставить их по 6 человек на стену. А после этого пришёл генерал и приказал расставить их по 7 человек на стену. И, наконец, явился маршал и приказал расставить их по 8 человек на стену. Коменданту удалось выполнить все эти приказы. Попробуйте и вы.

Задача 27.

Магазин купил у производителя наборы фломастеров и продает их по 100 рублей. Если покупатель приобретает сразу два набора фломастеров, то третий набор выдается ему в подарок. Известно, что магазин получает одну и ту же выгоду как от покупки одного набора, так и от покупки двух наборов. По какой цене магазин купил наборы фломастеров у производителя?

Задача 28.

В квадрат с длиной стороны 1 м вписали второй квадрат так, что его вершинами служат середины сторон первого. Во второй квадрат точно так же вписали третий. Найдите площадь третьего квадрата.

Задача 29.

У Пети в кармане несколько монет. Если Петя наугад вытащит из кармана 3 монеты, среди них обязательно найдётся монета в 1 рубль. Если Петя наугад вытащит 4 монеты из кармана, среди них обязательно найдётся монета в 2 рубля. Петя вытащил из кармана 5 монет. Можно ли точно сказать, что это за монеты?

Задача 30.

Имеются красный, синий, зелёный и чёрный шарики, среди которых могут быть волшебные. Детектор позволяет определить, сколько из помещённых в него шариков волшебны. Как узнать, какие шарики волшебные, а какие — нет, всего за три измерения?

Задача 21.

Петя посчитал, на каком этаже он живёт: если считать снизу, то на 33-м, а если считать сверху, то на 67-м. Сколько этажей в доме Пети?

Задача 22.

В комнате стоят табуретки и стулья. У каждой табуретки 3 ноги, у каждого стула 4 ноги. Когда на всех стульях и табуретках сидят люди, в комнате 49 ног. Сколько в комнате табуреток и сколько стульев?

Задача 23.

Плитка склеена из трёх равносторонних треугольников со стороной 1 см и имеет форму четырёхугольника со сторонами 1 см, 1 см, 1 см, 2 см. Можно ли такими плитками замостить равносторонний треугольник со стороной а) 12 см; б) 13 см?

Задача 24.

Перед Андреем и Серёжей на столе лежат три перевёрнутые карточки, под одной из которых написано «1», под второй «2» и под третьей «3». Андрей их перемешал и вытащил одну из них, но какую – Серёже не сказал. Серёжа может задать ему только один вопрос, на который тот, подумав, должен честно ответить «Да», «Нет» или «Не знаю», после чего Серёжа должен наверняка отгадать число, которое вытащил Андрей. Как ему это сделать?

Задача 25.

В записи 30 – 33 = 3 передвиньте одну цифру так, чтобы получилось верное равенство (менять местами две цифры нельзя!).

Задача 16.

Поезд длиною 180 м проезжает мимо фонаря за 9 секунд. За какое время он проедет мост длиною 360 м?

Задача 17.

Проверяя, что четырёхугольный кусок материи имеет форму квадрата, швея перегибает его по каждой диагонали и убеждается, что края оба раза совпадают. Обязательно ли кусок был квадратным, если он прошёл такую проверку?

Задача 18.

Год 2013 обладает тем свойством, что если его произнести по-американски, то есть «двадцать-тринадцать», то окажется, что число 2013 делится на 20 + 13, то есть на 33 (проверьте!). Квантик взял другое четырёхзначное число N, разбил его слева направо на двузначные числа и сложил – получилось число, делящееся на 33. Докажите, что и само число N тоже делится на 33.

Задача 19.

Маляр-хамелеон прыгает по клетчатой доске как обычная ладья (по горизонтали и вертикали на любое число клеток). Прыгнув в некоторую клетку, он либо перекрашивает её в свой цвет, либо сам перекрашивается в цвет этой клетки. Белого маляра-хамелеона поставили на чёрную доску 8 x 8 клеток. Может ли он раскрасить её в шахматную раскраску?

Задача 20.

Торговец принёс на рынок мешок орехов. Первый покупатель купил 1 орех, второй – 2 ореха, третий – 4, и так далее: каждый следующий покупатель покупал вдвое больше орехов, чем предыдущий. Орехи, купленные последним, весили 50 кг, после чего у торговца остался один орех. Сколько килограммов орехов было у торговца вначале? (Все орехи одинаковые.)

Задача 11.

Умный продавец получил для продажи несколько пачек конвертов по 100 конвертов в пачке. Десять конвертов он отсчитывает за десять секунд. У продавца попросили 60 конвертов. Сможет ли он отсчитать их быстрее, чем за минуту?

Задача 12.

Имеется много одинаковых клетчатых фигурок в виде буквы «Т» (см. рисунок). Можно ли из нескольких таких фигурок сложить такую же букву «Т», только большего размера? (В большой букве «Т» не должно быть дырок и перекрытий.)

Задача 13.

Между пятью ребятами произошёл разговор.
Андрей: «А я секрет знаю!»
Боря (Андрею): «Нет, не знаешь!»
Витя: «Борис, ты неправ!»
Гоша (Вите): «Это ты неправ!»
Дима: «Врёшь, Гоша!»
Известно, что больше половины ребят сказали правду. Знает ли Андрей секрет?

Задача 14.

Если Добрыня Никитич стукнет по чудо-берёзе, то с неё упадут яблоко и два банана. Если стукнет Илья Муромец — то яблоко и два апельсина. А если Алёша Попович — то яблоко, банан и апельсин. После того как богатыри постучали по чудо-берёзе, у них оказалось 2000 апельсинов, 1000 бананов и несколько яблок. А сколько?

Задача 15.

Настольные часы с часовой и минутной стрелками имеют форму куба с круглым циферблатом в центре одной из граней. На часах нет чисел и каких-либо пометок, показывающих, где у них верх. Поэтому можно случайно поставить их на бок или даже вверх ногами.
а) Какое время показывают часы на рисунке?
б) Есть ли в сутках хотя бы один такой момент, когда нельзя будет определить, какое время показывают эти часы?
В обоих пунктах считайте, что полдень уже наступил, а полночь ещё нет.

Задача 6.

К каждой грани кубика приклеили по такому же кубику. К каждой грани поверхности получившейся фигуры приклеили ещё раз по такому же кубику (при этом некоторые кубики закрыли две грани).
а) Сколько граней у полученного тела?
б) Из скольких кубиков состоит это тело?

Задача 7.

Квантик ввёл для себя режим: теперь только по средам, субботам и нечётным числам он читает Пушкина. Какое наибольшее количество дней подряд он может наслаждаться творениями великого поэта?

Задача 8.

Есть 101 монета. 100 из них одинаковые настоящие, а одна фальшивая, отличающаяся от настоящих по весу. Как с помощью двух взвешиваний на чашечных весах без гирь узнать, легче или тяжелее фальшивая монета, чем настоящая? (Находить фальшивую монету не требуется.)

Задача 9.

В слове КВАНТИК каждую букву заменили некоторой цифрой. Причём одинаковые буквы то есть (две буквы К) были заменены одинаковыми цифрами, а разные — разными. При этом оказалось, что выполняется следующее равенство:

Найдите, при каких значениях букв это возможно.

Задача 10.

В прежние времена, когда шариковых ручек ещё не было, ученики приносили в класс и ставили на парты чернильницы-непроливайки. Это такие сосуды, в которые легко окунуть перо, но при этом чернила из них не выливались, как их ни крути и ни опрокидывай. А как они были устроены? Придумайте и нарисуйте схему таких непроливаек.

Задача 1.

Арнольд Шварценеггер за один удар ломает кирпич на три меньших. За сколько ударов он сможет разбить один большой кирпич на 27 маленьких?

Задача 2.

Число-палиндром — это такое число, которое не меняется при записывании его цифр в обратном порядке. Чему равна сумма самого большого шестизначного палиндрома и самого маленького пятизначного?

Задача 3.

Коля и Петя играют в такую игру. На столе лежат 20 спичек. Первым ходит Коля. За один ход разрешается взять со стола одну или две спички.
а) Может ли Коля действовать так, чтобы взять последнюю спичку, независимо от игры Пети?
б) А может ли он действовать так, чтобы последнюю спичку взял Петя, как бы тот ни сопротивлялся?

Задача 4.

Из прямоугольника вырезали меньший прямоугольник и получили фигуру, изображённую на рисунке. Как с помощью карандаша и линейки провести прямую, которая делит площадь этой фигуры на две равные части?

Задача 5.

Коля и Вася за январь получили по 20 оценок, причём Коля получил пятёрок столько же, сколько Вася четвёрок, четвёрок столько же, сколько Вася троек, троек столько же, сколько Вася двоек, и двоек столько же, сколько Вася пятёрок. При этом средний балл за январь у них одинаковый. Сколько двоек за январь получил Коля?