Задача 46.

Король со свитой движется из пункта A в пункт B со скоростью 5 км/ч. Каждый час он высылает в пункт B гонцов, бегущих со скоростью 20 км/ч. С какими интервалами прибывают гонцы в пункт B?

Задача 47.

Нарисуйте на листе бумаги
а) 4 точки;
б) 5 точек;
в) 6 точек так, чтобы любые три из них были вершинами равнобедренного треугольника.

Задача 48.

В колонию из 100 черных бактерий попадает белая бактерия. Каждую секунду одна белая бактерия уничтожает одну чёрную бактерию, после чего все бактерии делятся надвое. Докажите, что рано или поздно все чёрные бактерии будут уничтожены, и выясните, в какой момент это произойдёт.

Задача 49.

На спортивном складе было поровну футбольных и волейбольных мячей. Когда из склада забрали часть волейбольных мячей, футбольных мячей стало в 7 раз больше, чем волейбольных. Когда затем изъяли еще 3 каких-то мяча, футбольных мячей стало в 20 раз больше, чем волейбольных. Сколько мячей было на складе первоначально?

Задача 50.

Решите ребус: МАТЕ x М = АТИКА. (Как обычно, одинаковыми буквами обозначены одинаковые цифры, а разными – разные.)

Задача 41.

Средний возраст 11 игроков футбольной команды равен 22 годам. Во время матча один игрок получил травму и ушёл с поля. Средний возраст оставшихся на поле игроков стал равен 21 году. Сколько лет футболисту, получившему травму?

Задача 42.

У окна стоят четыре девочки (см. рисунок). Каких двух девочек надо попросить повернуться, чтобы выяснить, истинно ли такое утверждение: «Если девочка без очков, то у неё в волосах бантик»?

Задача 43.

а) Можно ли в таблице размером 6 x 6 расставить числа так, чтобы сумма четырёх чисел в каждом квадрате 2 x 2 была отрицательной, а сумма всех чисел таблицы – положительной?
б) Решите ту же задачу для таблицы 5 x 5.

Задача 44.

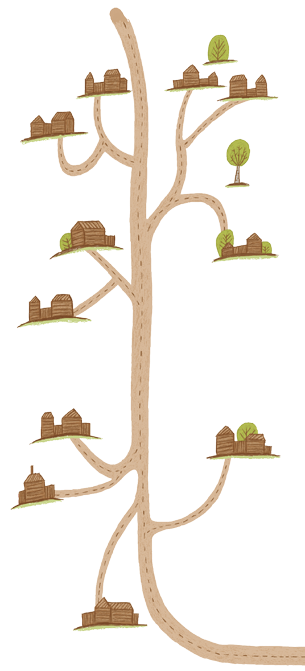
От шоссе отходят несколько дорог к сёлам (см. рисунок). Укажите на шоссе точку, в которой нужно расположить автобусную остановку, чтобы сумма расстояний от неё до сёл (по дорогам и шоссе) была наименьшей?

Задача 45.

На плоскости дана точка.
а) Нарисуйте на плоскости несколько кругов так, чтобы они не соприкасались ни с точкой, ни друг с другом, но «заслоняли» точку, то есть чтобы любой луч, выходящий из точки, упирался бы в один из кругов.
б) Какое наименьшее число кругов для этого потребуется?

Задача 36.

В стране три города: A, B и C. Жители города A всегда говорят правду, города B – лгут, а города C – строго попеременно лгут и говорят правду. В одном из городов случился пожар. Дежурному на каланче позвонили. Состоялся такой диалог:
– У нас пожар!
– Где горит?
– В городе C.
Куда ехать пожарным?

Задача 37.

Пешеход идёт вдоль шоссе с постоянной скоростью. Каждые 6 минут он видит попутный автобус, а каждые 3 минуты – встречный. Автобусы едут в обе стороны с одной и той же скоростью и отправляются из конечных пунктов через равные промежутки времени. Найдите эти промежутки.

Задача 38.

Коля и Вася зашли в магазин, где всё стоит целое число рублей. Коля купил 3 пачки сока и 4 булочки, после чего расплатился без сдачи несколькими 10-рублёвыми монетами. Вася же купил 9 пачек сока и 2 булочки. Докажите, что и он сможет расплатиться без сдачи 10-рублёвыми монетами.

Задача 39.

Петя нарисовал 5 рисунков. На каждом рисунке он изобразил несколько прямых и отметил все точки пересечения этих прямых друг с другом. В результате на первом рисунке он отметил всего 1 точку, на втором – 2, на третьем – 3, на четвертом – 4 и на пятом – 5.
а) Приведите примеры таких рисунков.
б) Про какие из Петиных рисунков можно наверняка сказать, сколько на них проведено прямых?

Задача 40.

Три одинаковые банки с тремя разными красками наполнены на две трети каждая. Есть возможность переливать любую часть жидкости из одной банки в другую (при этом краски, оказавшиеся в одной банке, равномерно перемешиваются). Как сделать во всех банках одинаковую смесь? (Другой посуды нет, выливать краску нельзя.)

Задача 31.

В двух сосудах находится по 1 л воды. Из первого сосуда переливают половину имеющейся в нём воды во второй сосуд, затем из второго переливают треть имеющейся в нём воды в первый, затем из первого переливают четверть имеющейся в нём воды во второй и так далее. Сколько воды окажется в каждом сосуде после 100 переливаний?

Задача 32.

Поверхность деревянного куба целиком окрасили. Затем куб распилили на несколько одинаковых кубиков. Оказалось, что среди них есть кубики с одной окрашенной гранью, причём их столько же, сколько кубиков, у которых все грани не окрашены. На сколько кубиков распилили куб?

Задача 33.

Два ртутных термометра висят так, как показано на рисунке. При какой температуре столбики ртути в них будут оканчиваться на одной высоте?

Задача 34.

Двое по очереди переводят часовую стрелку на 2 или 3 часа вперёд. Вначале часовая стрелка указывает на 6, победителем считается тот, после чьего хода она укажет на 12. (Стрелка может сделать несколько оборотов, прежде чем остановится на числе 12.) Кто из игроков – начинающий или его соперник – может обеспечить себе победу, и как ему играть?

Задача 35.

Докажите, что у правильной пятиконечной звезды, изображённой на рисунке, закрашена ровно половина площади.

Задача 26.

Маша покупала булочку ценой в целое число рублей. Ровно она заплатить не смогла и дала как можно меньшую сумму, но чтобы на булочку хватило. В итоге она дала продавщице 9 рублей и получила сдачу. Сколько стоила булочка?

Задача 27.

Окна в старых вагонах метро имеют форму, изображённую на рисунке справа. Закругления верхних углов рамы и стекла сделаны в виде дуги окружности. Окно приоткрыли, сдвинув стекло на 10 см. Высота подвижной части окна равна 25 см. Чему равна площадь открытой части окна?

Задача 28.

Шахматный конь захромал, и, делая обычный ход буквой Г, наступает на каждую клетку, входящую в эту букву (например, делая ход с a1 на b3, он наступает ещё и на клетки a2, a3, либо на b1, b2). Может ли хромой конь обойти поле 5 x 11 так, чтобы наступить на каждую клетку ровно один раз?

Задача 29.

Квантик попал на остров, населённый двумя племенами. Представители одного племени всегда говорят правду, представители другого — всегда лгут. Квантик подошёл к развилке дороги, и ему пришлось спросить у оказавшегося поблизости местного жителя, какая из двух дорог ведёт в деревню. Ему неизвестно, с представителем какого племени он разговаривает. Как, задав всего один вопрос, точно узнать, по какой дороге надо идти?

Задача 30.

На старой печатной машинке Незнайки на печать каждой конкретной цифры всегда расходуется одно и то же количество чернил. Незнайка говорит, что на этой машинке нельзя напечатать два натуральных числа, одно в 9 раз больше другого, истратив на каждое число одно и то же количество чернил. Не ошибается ли он?

Задача 21.

Петя и Вася живут в одном доме и выходят в школу одновременно. Каждый Петин шаг на 10% длиннее Васиного, но Петя делает в минуту на 10% меньше шагов, чем Вася. Кто из них раньше придёт в школу?

Задача 22.

Дан лист клетчатой бумаги. С помощью карандаша и линейки без делений нарисуйте на листе квадрат, площадь которого больше площади одной клетки а) в 2 раза; б) в 5 раз.

Задача 23.

Петя хочет придумать аналог игры «камень – ножницы – бумага» для 10 предметов. В ней должны выполняться два условия: про любые два предмета можно сказать, какой из них кого бьёт; любые два предмета равноправны (то есть каждый предмет бьёт одно и то же число предметов). Сможет ли Петя придумать такую игру?

Задача 24.

Имеется два дома, в каждом по два подъезда. Жильцы держат кошек и собак. Известно, что доля кошек (отношение числа кошек к общему числу кошек и собак) в первом подъезде первого дома больше, чем доля кошек в первом подъезде второго дома. А доля кошек во втором подъезде первого дома больше, чем доля кошек во втором подъезде второго дома. Верно ли, что доля кошек в первом доме больше доли кошек во втором доме?

Задача 25.

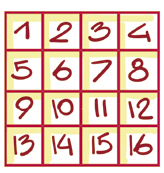
В таблицу 4 x 4 записали числа от 1 до 16 (так, как показано на рисунке). Перед каждым из них поставили знак «+» или «–» так, что в каждой строке и в каждом столбце оказалось по два плюса и по два минуса. Докажите, что сумма полученных чисел всегда будет равна нулю.

Задача 16.

Начнём считать пальцы на правой руке. Первым будет большой, вторым – указательный, третьим – средний, четвёртым – безымянный, пятым – мизинец, шестым – снова безымянный, седьмым – средний, восьмым – указательный, девятым – большой, деся- тым – указательный, и так далее. Какой палец будет тысячным?

Задача 17.

а) На столе лежат 3 яблока в 200 г, 300 г и 400 г. Карлсон, а затем Малыш берут по яблоку и одновременно начинают их есть (с одинаковой скоростью).Тот, кто доел своё яблоко, берёт следующее; каждый стремится съесть как можно больше. Какое яблоко должен взять Карлсон вначале?
б) А если имеется ещё яблоко в 450 г?

Задача 18.

В ряд слева направо стояли несколько столбов, между каждыми двумя соседними был натянут провод. Подул ветер, и все столбы упали влево, провода при этом не порвались и снова оказались натянутыми. Докажите, что все провода были привязаны к столбам параллельно земле.

Задача 19.

Известно, что вруны всегда врут, правдивые всегда говорят правду, а хитрецы могут и врать, и говорить правду. Вы можете задавать вопросы, на которые есть ответ «да» или «нет» (например: «Верно ли, что этот человек – хитрец?»). Перед вами трое – врун, правдивый и хитрец, которые знают, кто из них кто. Как и вам это узнать?

Задача 20.

Придумайте бумажную фигурку с таким свойством: её можно перегнуть по прямой так, что получится правильный треугольник, а можно перегнуть по прямой так, что получится прямоугольник.

Задача 11.

Профессор написал на доске шесть утверждений:
_Сегодня на моей лекции будет меньше 10 студентов.
Сегодня на моей лекции будет больше 10 студентов.
Сегодня на моей лекции будет меньше 20 студентов.
Сегодня на моей лекции будет больше 20 студентов.
Сегодня на моей лекции будет меньше 30 студентов.
Сегодня на моей лекции будет больше 30 студентов.
_На лекцию пришло N студентов, после чего профессор написал для каждого своего утверждения, верное оно или нет. Оказалось, что ровно четыре утверждения оказались неверными. Чему равно N? Укажите все возможные ответы.

Задача 12.

В классе у Коли столько же детей, сколько в классе у Оли. Коля говорит Оле: «У нас в классе мальчиков вдвое больше, чем у тебя». А Оля отвечает: «Зато у нас девочек втрое больше, чем у тебя». Могло ли такое быть? (Коля и Оля себя тоже посчитали).

Задача 13.

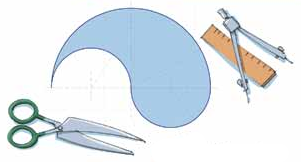
Перед вами рисунок «капли» – верхняя граница состоит из полуокружности радиуса 2, а нижняя граница – из двух полуокружностей радиуса 1 (одна «смотрит» внутрь капли, а другая – «наружу»). Разрежьте каплю
а) на две одинаковые части;
б) на три одинаковые части;
в) можно ли разрезать её на 100 равных частей?

Задача 14.

В таблице 10 x 10 клетки окрашены в 9 цветов. Если в некоторой строке или в некотором столбце находятся две клетки одного цвета, то можно перекрасить этот столбец или эту строку в этот цвет. Из любого ли исходного положения можно всю таблицу перекрасить в один цвет?

Задача 15.

Бизнесмен заключил с чёртом соглашение: каждый день бизнесмен даёт чёрту одну купюру, а взамен получает любое число купюр, какое захочет, но меньшего достоинства. Другого источника купюр у бизнесмена нет. Докажите, что в какой-то момент бизнесмен разорится (сколько бы купюр ни было у него вначале и как бы он ни менял их у чёрта).

Задача 6.

Даны три целых числа. Ни одно из первых двух не делится на третье, а произведение первых двух делится на квадрат третьего числа. Может ли такое быть?

Задача 7.

Велосипедисты Алёша, Боря и Вася одновременно стартуют из одной и той же точки кольцевого трека (скорость каждого постоянна). Первыми после старта проехали мимо друг друга Алёша и Боря (в одну сторону или в разные – неизвестно). Известно, что Алёша едет по часовой стрелке, а Вася против часовой стрелки. В каком направлении едет Боря?

Задача 8.

Двое играют в упрощённый морской бой. В таблице размером 4 x 4 клетки расположен один корабль размером 1 x 3 клетки.
а) Приведите пример залпа из пяти снарядов, который обязательно заденет корабль, где бы он ни располагался.
б) Обязательно ли найдётся аналогичный залп из четырёх снарядов?

Задача 9.

В клуб пришли 20 джентльменов: некоторые – в шляпах, некоторые – без. Затем время от времени один из джентльменов снимал с себя шляпу и надевал на голову другому джентльмену, у которого в этот момент шляпы не было. Через час десять джентльменов заявили: «Я отдавал шляпу чаще, чем получал!» Сколько джентльменов пришли в клуб в шляпах?

Задача 10.

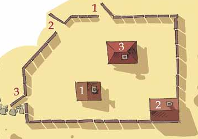
Во дворе, окружённом забором с тремя калитками, стоят три домика. На домиках и калитках написаны номера. Можно ли провести от каждого домика дорожку к калитке с тем же номером так, чтобы дорожки не пересекались?

Задача 1.

В клетке было 7 верблюдов и работник зоопарка Вениамин. Каждый верблюд плюнул 3 раза и получил 2 плевка от товарищей. Сколько плевков получил Вениамин? (Верблюды не промахиваются и выбирают цель для плевка только внутри клетки. Вениамин не плюётся.)

Задача 2.

Однажды я жарил оладьи. Когда я начал переворачивать одну из них, она никак не входила на старое место. Оладьи удалось вновь разместить на сковороде, лишь перевернув их все.
а) Докажите, что всегда можно уложить перевернутые оладьи на круглой сковороде, на которой они лежали раньше.
б) Приведите пример, в котором нельзя ни одну из оладий, перевернув, уложить на старое место.

Задача 3.

На физическом кружке учитель поставил такой эксперимент. Он разместил на чашечных весах 16 гирек массами 1, 2, 3, … , 16 граммов так, что одна из чаш перевесила. Пятнадцать учеников по очереди выходили из класса и забирали с собой по одной гирьке, причём после выхода каждого ученика весы меняли своё положение (каждый раз перевешивала не та чаша весов, что в предыдущий раз). Какая гирька могла остаться на весах (укажите все возможности)?

Задача 4.

Какое наибольшее число белых шашек можно расставить на доске 8 x 8 так, чтобы поставленная в некоторую клетку чёрная шашка смогла побить их все за один ход?

Задача 5.

Билет на проезд в общественном транспорте считается счастливым, если в его шестизначном номере сумма первых трёх цифр равна сумме последних трёх цифр.
Как-то между тремя приятелями состоялся такой разговор:
– Однажды мне попался счастливый билет, у которого каждая цифра начиная со второй была либо вдвое больше, либо вдвое меньше предыдущей, – заявил Петя.
– А мне, помню, достался счастливый билет, у которого каждая цифра начиная со второй была либо вдвое больше, либо втрое меньше преды­ ущей, – сообщил Коля.
– А у моего счастливого билета каждая цифра начиная со второй была либо вдвое больше, либо вчетверо меньше предыдущей, – сказал Вася.
Чьи слова могли быть правдой?

Задача 6.

Даны три целых числа. Ни одно из первых двух не делится на третье, а произведение первых двух делится на квадрат третьего числа. Может ли такое быть?
Попробуйте разобраться в такой ситуации:
6-Д. а) Найдутся ли 5 разных натуральных чисел, ни одно из которых не квадрат целого числа, но произведение любых двух из них – квадрат целого числа?
б) Тот же вопрос, но требуется, чтобы произведение любых трёх из этих чисел было квадратом целого числа.

Задача 19.

Известно, что вруны всегда врут, правдивые всегда говорят правду, а хитрецы могут и врать, и говорить правду. Вы можете задавать вопросы, на которые есть ответ «да» или «нет» (например: «Верно ли, что этот человек – хитрец?»). Перед вами трое – врун, правдивый и хитрец, – и они знают, кто из них кто. Как и вам это узнать?
19-Д. А если перед вами четверо – врун, правдивый и два хитреца (все четверо знают, кто из них кто)? Докажите, что хитрецы могут договориться отвечать так, что вы, спрашивая этих четверых, ни про кого из них не узнаете наверняка, кто он!

Задача 22.

Дан лист клетчатой бумаги. Имея в наличии только линейку без делений и карандаш, нарисуйте на листе квадрат, площадь которого больше площади одной клетки: а) в 2 раза; б) в 5 раз.
В решении этой задачи мы строили нужный квадрат, соединяя узлы клетчатой бумаги.
22-Д. А для каких целых чисел N найдётся квадрат с вершинами в узлах клетчатой бумаги, площадь которого больше площади клетки в N раз?

Ответ довольно неожиданный: число N должно представляться в виде суммы двух квадратов целых чисел. Например, в исходной задаче 2=1² + 1², а 5=1² + 2². Постройте искомый квадрат для N=10=1² + 3² и N=13=2² + 3² и попробуйте доказать общее утверждение.
Подсказка: вам поможет теорема Пифагора.

Задача 29.

Квантик попал на остров, населённый двумя племенами. Представители одного племени всегда говорят правду, представители другого – всегда лгут. Квантик подошёл к развилке дороги, и ему пришлось спросить у оказавшегося поблизости местного жителя, какая из двух дорог ведёт в деревню. Ему неизвестно, с представителем какого племени он разговаривает. Как, задав всего один вопрос, точно узнать, по какой дороге надо идти?
29-Д. А если аборигены говорят на местном языке, в котором есть слова «пиш» и таш», означающие «да» и «нет»? Квантик знает этот язык, но забыл, что именно из «пиш» и таш» означает «да», а что – «нет». Как за один вопрос, ответом на который будет «да» или «нет» (вернее, «пиш» или «таш»), узнать, какая дорога ведёт в деревню?

Задача 45.

a) На плоскости дана точка. Нарисуйте на плоскости несколько кругов так, чтобы они не соприкасались ни с точкой, ни друг с другом, но «заслоняли» точку, то есть чтобы любой луч, выходящий из точки, упирался бы в один из кругов.
б) Какое наименьшее число кругов для этого потребуется?
Оказывается, хватит всего трёх кругов. А что, если поставить аналогичную задачу для пространства?
45-Д. В пространстве дана точечная лампочка, светящая во все стороны. Придумайте, как подобрать четыре непрозрачных шара и расположить их в пространстве, чтобы они не соприкасались ни друг с другом, ни с лампочкой, но полностью загораживали свет от неё (то есть чтобы любой луч, выходящий из лампочки, упирался бы в один из этих шаров)?

А вот ещё похожий по виду вопрос: можно ли заслонить точечную лампочку на плоскости зеркальными кругами? Лампочка светит во все стороны, но если её луч упирается в круг, то он отражается от круга (по закону «угол падения равен углу отражения»). Можно ли так расположить круги, чтобы ни один луч не ушёл за пределы кругов, а всё время отражался бы от них? Оказывается, эта задача до сих пор не решена! Более подробно об этом рассказано в мультфильме «Экранировать луч» на сайте «Математические этюды» (etudes.ru).

Напоследок приведём задачу, которая уже была в конкурсе этого года, но в другой формулировке:
??-Д. На столе лежат четыре карточки, как показано на рисунке. На каждой карточке с одной стороны – буква, а с другой – натуральное число. Какие карточки надо перевернуть, чтобы узнать, правда ли, что если на какой-то стороне карточки написано чётное число, то на другой стороне – гласная буква?
Решите эту задачу и догадайтесь, под каким номером в конкурсе она была.