Математический конкурс 2017/18 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (ученик 6 класса Михаил Энгельгардт)
Можно ли сложить из нескольких различных равнобедренных прямоугольных треугольников фигуру, все стороны которой идут по линиям квадратной сетки?

Задача 57. (Мария Ахмеджанова)
Чему равняется БИТ, если БИТ × 8 = БАЙТ и Б + А + Й + Т = 8?
(Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными – разные, и ни одно многозначное число не начинается с ноля.)

Задача 58. (Мария Ахмеджанова)
На острове рыцарей и лжецов путешественник встретил четверых местных жителей. Он задал каждому из них один и тот же вопрос – то ли «Сколько лжецов среди вас четверых?», то ли «Сколько лжецов среди троих остальных?» – и получил такие ответы:
1) «Все»; 2) «Больше половины»; 3) «Ровно половина»; 4) «Только один».
Можно ли установить а) какой из вопросов задавал путешественник; б) кто из островитян рыцарь, а кто – лжец? (Рыцари всегда говорят правду, лжецы всегда лгут.)

Задача 59. (Сергей Костин)
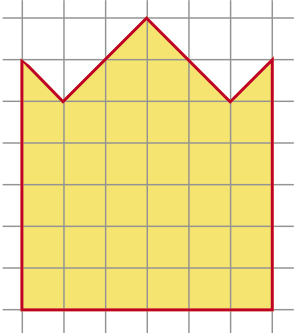
Во всех клетках квадрата 5×5 написаны числа. Известно, что сумма всех чисел равна 77, а сумма чисел, написанных в клетках любого прямоугольника 1×3 или 3×1, целиком расположенного внутри квадрата, равна 10. Найдите сумму чисел, написанных
а) в угловых клетках квадрата;
б) в клетках, которые выделены цветом на рисунке.


Задача 60. (Александр Грибалко)
Шахматного коня требуется поставить на одну из клеток доски n×n и сделать им n – 1 ходов так, чтобы он побывал на каждой горизонтали и на каждой вертикали. При каких n это возможно?

XI тур
Задача 51. (Александр Грибалко)
Двум братьям сейчас 25 и 36 лет. Они заметили, что оба их возраста одновременно являются точными квадратами. Могло ли с ними такое быть и раньше?

Задача 52. (ученик 6 класса Михаил Энгельгардт)
По контуру клетчатого квадрата 11x11 отмечены узлы сетки. Играют двое. Первый проводит во внутренней клетке квадрата диагональ, один конец которой уже отмечен, а второй конец – ещё нет, и отмечает второй конец. Второй игрок проводит диагональ клетки, соединяющую отмеченные узлы. Запрещается в одной клетке проводить две диагонали. Кто не может сделать ход, проигрывает. Кто из игроков может обеспечить себе победу, как бы ни играл его соперник?

Задача 53. (Алексей Заславский)
Два джентльмена прогуливаются по бульвару. Они начали прогулку одновременно из противоположных концов и впервые встретились в 50 метрах от середины бульвара. Дойдя до конца бульвара, каждый сразу поворачивает и идёт обратно с той же скоростью. Джентльмены встретились лицом к лицу ещё дважды, после чего один догнал другого в конце бульвара. Найдите длину бульвара.

Задача 54. (Арсений Акопян)
Можно ли так «перемешать» кубик Рубика, что все цвета останутся прежними, кроме центральных квадратиков – те поменяют цвет на цвет противоположного квадратика?

Задача 55. (Константин Кноп)
В непрозрачном мешке лежат в беспорядке фигурки пентамино 12 разных цветов, по 12 комплектов каждого цвета, – всего 1728 фигурок. Незнайка наугад достаёт одну за другой пентаминошки из мешка. Его цель – либо отыскать по одному экземпляру 12 фигурок разной формы (не важно, какого цвета), либо 12 каких угодно одноцветных фигурок, либо 12 одинаковых по форме фигурок каких угодно цветов. Какое наименьшее число фигурок должен вытащить Незнайка, чтобы гарантированно достичь цели?

X тур
Задача 46. (Сергей Шашков)
Расшифруйте ребус АХ + ОХ = ОДА. (Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными – разные, и ни одно число не начинается с ноля.)

Задача 47. (Егор Бакаев)
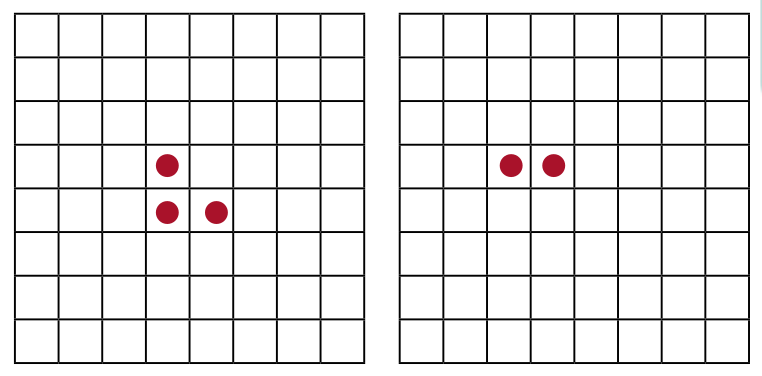
На клетчатой доске стоят три фишки (как показано на левом рисунке). Одним ходом можно одновременно передвинуть одну фишку вверх (на одну клетку), одну фишку влево (на одну клетку) и одну фишку по диагонали вправо-вниз (на одну клетку). После нескольких таких ходов две фишки встали, как показано на правом рисунке. Где могла оказаться третья фишка?

Задача 48. (Евгений Братцев)
Олег устраивает вечеринки исключительно по пятницам 13-го. Мог ли он остаться без вечеринок в каком-нибудь году? А какое наибольшее число вечеринок может быть у Олега за год?

Задача 49. (Егор Бакаев)
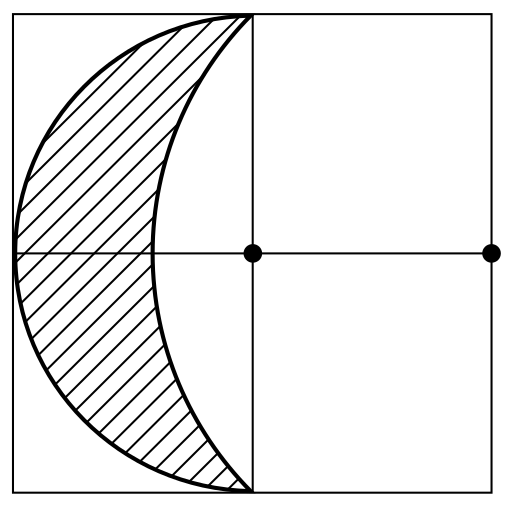
На клетчатой бумаге провели две окружности с центрами в отмеченных точках. Их дуги ограничивают заштрихованную фигуру. Найдите её площадь, если площадь одной клетки равна 1.

Задача 50. (Михаил Евдокимов)
У эксперта есть 8 золотых пластин, промаркированных 10 г, 20 г, 30 г, 40 г, 50 г, 60 г, 70 г и 80 г, а также слабочувствительные двухчашечные весы без гирь. Более тяжёлая чашка этих весов перевесит, если разность весов на чашках больше 10 г, иначе весы останутся в равновесии. Эксперт знает, что вес ровно одной из пластин меньше заявленного. Как ему определить эту пластину на таких весах за 3 взвешивания?

IX тур
Задача 41. (Евгений Смирнов)
Юра смотрит на календарь, открытый на каком-то месяце, и говорит: «если к четвергу прибавить субботу, получится вторник». Какой сейчас месяц, если дело происходит в 2018 году?

Задача 42. (Михаил Евдокимов)
Бен Ганн помнит, что Флинт зарыл свои сокровища, когда прошёл от высокой сосны, растущей в глубине острова, 10, 20, 30 и 40 ярдов в четырёх различных направлениях (север, юг, восток и запад), но не помнит, в каком именно порядке это было. Бен находится с компасом у той самой сосны. Сколько ям ему нужно выкопать, чтобы наверняка найти сокровища Флинта?

Задача 43. (Михаил Евдокимов)
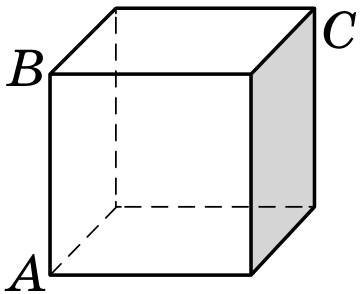
Планета Плюк имеет форму куба, в трёх вершинах которого находятся города A, B и C (см. рисунок). Где нужно построить космодром так, чтобы расстояние от космодрома по поверхности планеты до городов было одинаковым? Укажите все варианты.

Задача 44. (Евгений Смирнов)
У Жени есть 10 кубиков, занумерованных цифрами от 0 до 9. Он отложил кубик с нулём и сложил остальные кубики в виде магического квадрата 3×3. Потом Женя потерял один кубик, но, используя отложенный кубик с нулём, снова сложил магический квадрат 3×3. Какой кубик потерял Женя? Укажите все возможности и докажите, что других нет.

Задача 45. (Александр Шаповалов)
Какое наибольшее число слонов можно расставить на шахматной доске так, чтобы каждый бил не более одного другого? (Приведите пример расстановки и докажите, что большее число слонов расставить нельзя.)

VIII тур
Задача 36. (Михаил Евдокимов)
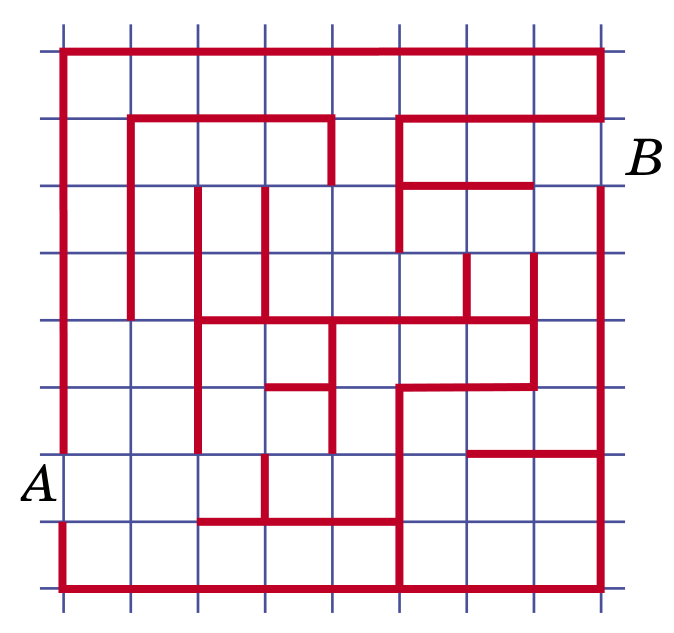
Перед вами рисунок лабиринта. В нём разрешается сломать одну из перегородок между клетками. Сделайте это так, чтобы длина кратчайшего пути по клеткам от выхода A к выходу B была наименьшей. Не забудьте обосновать ответ.

Задача 37. (Алексей Заславский)
В Шиловске шило стоит на 1% дешевле, чем в Мыловске, а мыло – на 1% дороже. Проезд из одного города в другой стоит 1000 рублей. У юного бизнесмена, живущего в Шиловске, есть 100 тысяч рублей и он мечтает разбогатеть, меняя шило на мыло. Сбудутся ли его мечты?

Задача 38. (Александр Шаповалов)
Можно ли квадрат разрезать на трапеции, в каждой из которых есть угол 179°?

Задача 39. (Сергей Шашков)
Расшифруйте ребус
НЕ + МНЕ = ЕМУ.
(Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными – разные, и ни одно число не начинается с ноля.)

Задача 40. (Григорий Гальперин)
Гравировщик шлифует алмаз, имеющий форму выпуклого многогранника, превращая его постепенно в бриллиант. Начинает он с того, что сначала срезает все уголки алмаза-многогранника (маленькие пирамидки при вершинах) остро отточенным плоским ножом. Докажите, что после этой операции число вершин у полученного многогранника будет чётным, а число рёбер – делиться на 3.

VII тур
Задача 31. (Егор Бакаев)
Разрежьте фигурку на рисунке на 5 одинаковых частей.

Задача 32. (Григорий Гальперин)
Количество цифр в числе N в 2018 раз меньше, чем само число N. Чему может равняться N? (Найдите все возможные варианты и докажите, что других нет.)

Задача 33. (Сергей Костин)
Два игрока по очереди нанизывают красные, синие и зелёные кольца на 33 стержня. У каждого игрока неограниченное количество колец каждого типа. За ход игрок нанизывает какое-либо кольцо на какой-то стержень. Запрещается помещать красное кольцо непосредственно на синее, а синее – непосредственно на зелёное. Также на стержне не может быть более одного кольца каждого цвета. Проигрывает тот, кто не может сделать ход. Кто из игроков может всегда выигрывать, как бы ни играл его соперник?

Задача 34. (Гриша Никитин)
а) Петя пишет в каждой клетке доски 100×100 буквы А или Б так, чтобы всего на доске их было поровну. Вася передвигает по этой доске фишку, сдвигая её всё время только в соседнюю клетку и каждый раз записывая, на какой букве она стоит. Всегда ли Вася может так поставить фишку и так обойти ею все клетки ровно по одному разу, чтобы полученная последовательность букв одинаково читалась слева направо и справа налево?
б) То же самое для доски 101×101, букв А на одну больше, чем букв Б.

Задача 35. (Игорь Акулич)
– Поделил я как-то одно натуральное число на другое с остатком, – рассказывал Петя Коле. – Когда же я поделил квадрат первого числа на второе, остаток оказался вдвое больше, чем был при первом делении. А когда я поделил куб первого числа на второе, остаток стал уже втрое больше.
– Ну, это ты заливаешь, такого не может быть! – воскликнул Коля. – Вот со мной действительно была похожая история. Я тоже поделил одно натуральное число на другое с остатком. И когда я поделил куб первого числа на второе, остаток оказался вдвое больше первоначального, а когда поделил квадрат первого числа на второе, остаток стал втрое больше.
– Теперь уже ты сочиняешь! – заявил Петя.
Кто мог быть прав в каждом случае?

VI тур
Задача 26. (Борис Френкин)
На гранях кубика написаны натуральные числа от 1 до 6 в каком-то порядке. Если на двух соседних гранях стоят соседние числа (то есть отличающиеся на 1), то покрасим ребро между ними в красный цвет, а в противном случае – в синий. Каково наименьшее возможное количество красных рёбер?

Задача 27. (Константин Кноп)
На кинопремию «Оскар» были выдвинуты пять режиссёров, но получил её только один. Когда у каждого из них спросили, кто получил премию, первый режиссёр назвал себя, второй режиссёр назвал себя и ещё одного режиссёра, третий – себя и ещё двоих, четвёртый – себя и трёх других, а пятый – всех пятерых. Впоследствии выяснилось, что ни у каких режиссёров не оказалось равного числа людей, названных ошибочно (которые не получили премию). Кто получил «Оскар»?

Задача 28. (Григорий Гальперин)
Выпишем по возрастанию все положительные несократимые дроби, меньшие 1, знаменатели которых меняются от 2 до 2018. Чему равно среднее арифметическое этих дробей?

Задача 29. (Григорий Гальперин)
Можно ли разрезать квадрат на конечное число а) правильных пятиугольников; б) выпуклых пятиугольников?

Задача 30. (Игорь Акулич)
Треугольным называют число, равное сумме всех натуральных чисел от 1 до какого-то натурального числа включительно. Вот первые несколько треугольных чисел: 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, и т.д. Петя, исследуя их свойства, сформулировал две теоремы:
I. I. Если сумма двух треугольных чисел является степенью двойки, то и их разность является степенью двойки.
II. Если разность двух треугольных чисел является степенью двойки, то и их сумма является степенью двойки.
Верна ли хотя бы одна из этих теорем? А может быть, обе?

V тур
Задача 21. (Александр Домашенко)
Читая книгу Мартина Гарднера, Настя заметила, что её папе в n2 году исполнится n лет. Сколько лет исполняется отцу в 2018 году?

Задача 22. (Александр Перепечко)
Марсианская роза каждую ночь меняет свою высоту. Если высота была не больше метра, то она удваивается, иначе – уменьшается на метр. Спутник пролетает над розой каждый третий день. Может ли он каждый раз видеть розу одной и той же высоты?

Задача 23. (Данила Боханов, ученик 7 класса)
Петя придумал признак равенства четырёхугольников. Он утверждает, что если даны четырёхугольники ABCD и A’B’C’D’ (не обязательно выпуклые), причём три стороны одного соответственно равны трём сторонам другого (AB = A’B’, BC = B’C’, CD = C’D’) и диагонали одного соответственно равны диагоналям другого (AC = A’C’, BD = B’D’), то и сами четырёхугольники равны. Не ошибается ли Петя?

Задача 24. (Михаил Евдокимов)
Квадрат 5×5 разбили на единичные квадратики и в каждом из них одним из двух возможных способов провели диагональ. Получилось какое-то разбиение исходного квадрата на 50 маленьких треугольников. Всегда ли удастся окрасить 25 треугольников в чёрный цвет так, чтобы чёрные треугольники не имели общих сторон?

Задача 25. (Александр Перепечко)
В куче 131 камень. Двое берут камни по очереди. Сначала первый игрок берёт k камней, где k – некоторое фиксированное число. Каждым следующим ходом игрок берёт либо столько же камней, сколько брал его соперник на предыдущем ходу, либо на один больше. Кто не может сделать ход – проиграл. Кто из игроков может гарантировать себе победу, как бы ни играл его соперник, если а) k = 9? б) k = 1?

IV тур
Задача 16. (Борис Френкин)
На острове три селения. В одном из них живут рыцари, в другом разбойники, в третьем торгаши. Рыцари всегда говорят правду, разбойники всегда лгут, а торгаши могут как сказать правду, так и солгать. Путешественник поговорил с тремя туземцами А, Б, В из трёх разных селений, не зная, кто откуда. Туземец А сказал, что Б рыцарь; Б сказал, что В разбойник; В сказал, что А торгаш. Солгал ли торгаш?

Задача 17. (Михаил Евдокимов)
На доске написано десятизначное число. Все его цифры различны. Может ли оказаться, что, вычеркнув две его последние цифры, получим число, делящееся на 2, вычеркнув три его последние цифры, получим число, делящееся на 3, …, вычеркнув 9 его последних цифр, получим число, делящееся на 9?

Задача 18. (Михаил Евдокимов)
На каждой клетке квадратной доски 10×10 стоит чёрная или белая фишка, причём всего тех и других поровну. Разрешается поменять местами две разноцветные фишки, стоящие рядом (в соседних по стороне клетках), или убрать с доски две одноцветные фишки, стоящие рядом. Верно ли, что всегда возможно убрать все фишки с доски, действуя по правилам, как бы фишки ни были расположены вначале?

Задача 19. (Александр Домашенко)
Николаю Ивановичу – любителю занимательных задач – нравится наряжать игрушками-головоломками новогоднюю ёлку для внуков. Он приготовил из плотной бумаги правильный тетраэдр (треугольную пирамидку из равносторонних треугольников). Затем разрезал его хитрым способом и получил ёлочку (она составлена симметрично из трёх равных половинок правильного шестиугольника, см. рисунок). Как ему это удалось?

Задача 20. (Игорь Акулич)
В школьном химическом кабинете имеются двухчашечные весы с набором из 20 гирек массами 1 г, 2 г, …, 20 г. Коля разложил все эти гирьки по чашкам весов так, что они уравновесились. Петя хочет убрать часть гирек так, чтобы равновесие сохранилось. Какое наименьшее количество гирек ему потребуется снять, чтобы гарантированно добиться успеха (как бы ни были разложены гирьки по чашкам)?

III тур
Задача 11. (Григорий Гальперин)
В ряд стоят 100 шкатулок, в них всего 2017 монет. На каждой шкатулке написано: «В какой-то из остальных шкатулок не меньше одной монеты». Известно, что не все надписи правдивы, а в шкатулке №37 есть хотя бы одна монета. Сколько монет в каждой из шкатулок?

Задача 12. (Сергей Дворянинов)
Из чисел 1, 2, 3, …, 998, 999 выбрали 997 чисел. Оказалось, что их сумма делится на 500, но не делится на 1000. Какое число заведомо присутствует среди выбранных?

Задача 13. (Егор Бакаев)
Несколько ребят сходили в лес по ягоды. Оказалось, что все собрали ягод поровну. Алёша нашёл 1/9 всех собранных ягод черники и 1/11 всех собранных ягод брусники. Ягоды других видов ребята не собирали. Докажите, что Алёша собрал столько же ягод брусники, сколько черники.

Задача 14. (ученик 7 класса Богдан Цыганов)
«Лесенка» состоит из тех клеток квадрата 10х10, которые лежат на главной диагонали или под ней. Может ли король обойти всю эту фигуру, начав с некоторой клетки, не посещая никакую клетку дважды и делая только горизонтальные и диагональные ходы на соседние клетки (нельзя делать ход на клетку, соседнюю по вертикали)?

Задача 15. (Фёдор Нилов)
Оказалось, что в группе по изучению французского языка для любых двух девочек есть ровно один мальчик, который нравится им обеим, и каждый мальчик нравится по крайней мере трём девочкам. Приведите пример такой группы, в которой учится больше одного мальчика.

II тур
Задача 6. (Лёва Зенков, 8 лет)
Пятачок и Винни Пух вышли из дома Пятачка и пошли купаться на озеро, двигаясь с одной и той же скоростью. Через 15 минут, на полпути от дома до озера, Пятачок обнаружил, что забыл плавки, и побежал с вдвое большей скоростью домой и обратно к озеру, нигде не задерживаясь по дороге. Насколько позже Винни-Пуха Пятачок оказался на озере?

Задача 7. (Мария Ахмеджанова)
Чему равняется сумма ТЫР + ПЫР, если известно, что ТЫР + ПЫР = 8 × ДЫР? (Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными – разные, и ни одно число не начинается с ноля.)

Задача 8. (Мария Ахмеджанова)
Провожая трёх своих внуков к родителям, бабушка дала им в дорогу три пирога: с картошкой, с вареньем и с грибами. В поезде пироги были съедены, причём каждый пирог ели двое внуков. При этом тому из внуков, который терпеть не может пирогов с картошкой, не досталось и пирога с грибами. Сашенька не ел пирога с вареньем. Кто какие пироги ел, если Вовочка участвовал в поедании большего числа пирогов, чем Петенька?

Задача 9. (Арсений Акопян, Константин Кноп)
Известно, что несколько небольших тяжёлых ящиков можно увезти на семи 6-тонных грузовиках, но нельзя увезти на меньшем количестве таких грузовиков. Докажите, что этот груз не удастся увезти \n а) на трёх 7-тонных грузовиках, \n б) на трёх 9-тонных грузовиках.

Задача 10. (Михаил Евдокимов)
Три прямые дорожки парка образуют треугольник. В парке три входа – они расположены в серединах дорожек, а в каждой вершине расположен фонарь. От каждого из входов нашли кратчайшее расстояние до наиболее удалённого фонаря, если идти по дорожкам. Оказалось, что два из трёх полученных чисел равны. Обязательно ли тогда длины каких-то двух дорожек равны?

I тур
Задача 1. (Сергей Волчёнков)
Когда поезд едет из Москвы в Ярославль, буфет находится в 7-м вагоне от головы, а когда из Ярославля в Москву – в 13-м. Cколько вагонов в этом поезде?

Задача 2. (Михаил Евдокимов)
У Умного Кролика есть участок квадратной формы 8х8, состоящий из 64 одинаковых грядок 1х1. На некоторых грядках он выращивает капусту, а на остальных морковь (пустых грядок нет). Известно, что рядом с каждой капустной грядкой ровно две капустные, а рядом с каждой морковной ровно две морковные (грядки находятся рядом, если они соседние по стороне). Может ли доля капустных грядок составлять а) ровно половину; б) более 60% от общего числа грядок?

Задача 3. (Виктор Дрёмов и Александр Перепечко)
В тайную лабораторию собираются послать 10 существ, часть из них – сумасшедшие учёные, остальные – безрукие големы. В течение недели каждое утро каждый учёный будет пришивать каждому голему по одной новой руке, после чего големы пойдут на алмазные копи и вечером принесут оттуда по алмазу в каждой руке. Сколько должно быть сумасшедших учёных, чтобы големы насобирали за неделю максимальное количество алмазов?

Задача 4. (Константин Кноп и Ксения Рушинская)
Имеются 100 шариков, из которых два титановых, а остальные нет. Титан-тестер умеет за одну проверку тестировать ровно два шарика. Если хотя бы один из шариков титановый, у тестера загорается лампочка (иначе лампочка не горит). Как найти оба титановых шарика за 52 проверки?

Задача 5.
а) Квадрат площади 10 разрежьте на несколько частей, из которых можно сложить прямоугольник 2х5.
б) Существует ли такое разрезание этого квадрата всего на три части?
(При подготовке разрезания используйте, если нужно, карандаш, линейку и циркуль.)


