Математический конкурс 2018/19 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (Александр Перепечко)
Кузнечик прыгает по узлам клетчатой плоскости. Он может перепрыгнуть из одного узла в другой, если расстояние между ними (по прямой) равно 5 (сторона клетки имеет длину 1). В любой ли узел плоскости может попасть кузнечик?

Задача 57. (Григорий Гальперин)
Барон Мюнхгаузен составил квадратную таблицу умножения чисел от 1 до 100 – в каждой клетке таблицы 100×100 записал произведение номеров строки и столбца, в которых стоит эта клетка. Барон утверждает, что сумма всех полученных произведений – квадрат целого числа. Прав ли барон?

Задача 58. (Алексей Воропаев)
Квантик и Ноутик играют на белой клетчатой доске 17×17. За ход надо закрасить в чёрный цвет состоящий из белых клеток многоугольник площади не более 9. Проигрывает тот, кто не может сделать ход, начинает Ноутик. Кто из играющих может обеспечить себе победу и как ему играть?

Задача 59. (Сергей Костин)
На прямой отмечено несколько точек. За ход между каждой парой соседних точек ставится одно и то же количество новых точек: 3, 4 или 5 (для очередного хода можно выбирать какое-то одно из этих чисел). Может ли на прямой после нескольких таких ходов (не менее одного) оказаться ровно 333444555 отмеченных точек?

Задача 60. (Константин Кноп)
Найдите углы треугольника, если его медиана образует со сторонами, выходящими из той же вершины, углы 15° и 30°.

XI тур
Задача 51. (Игорь Акулич)
Как поётся в русской народной песне, «три деревни, два села, восемь девок, один я» – и в каждом из указанных населённых пунктов кто-то из нас живёт. При этом в любой деревне больше девок, чем в любом селе. А Новый год мы всегда празднуем в том единственном месте, где проживает больше всего девок. Где живу я – в деревне или в селе?

Задача 52. (Григорий Гальперин)
Среди 111 монет часть – настоящие и весят одинаково, а остальные – фальшивые и тоже весят одинаково, но они легче настоящих. Монеты разложили на чашечные весы, на левую чашку – 60 монет, на правую – 51 монету, и весы пришли в равновесие. Какое а) наименьшее; б) набольшее число фальшивых монет могло быть? В каждом случае определите, во сколько раз фальшивая монета легче настоящей.

Задача 53. (Александр Перепечко)
В клетчатой таблице 8×8 строки и столбцы пронумерованы числами от 1 до 8. Квантик отметил некоторые клетки так, что количество отмеченных клеток в каждой строке не больше номера строки, а в каждом столбце – не меньше номера столбца. Сколько всего клеток он мог отметить?

Задача 54. (Сергей Костин)
К некоему натуральному числу каждую секунду прибавляют 67, 78 или 89. Докажите, что когда-нибудь обязательно получится число, десятичная запись которого заканчивается на 67, 78 или 89.

Задача 55. (Лев Емельянов)
Верно ли, что из пяти диагоналей каждого невыпуклого пятиугольника можно выбрать три, из которых складывается треугольник? (Диагональ – это отрезок, соединяющий несоседние вершины, некоторые диагонали будут лежать вне пятиугольника.)

X тур
Задача 46. (Александр Блинков)
Саша придумал признак равенства тупоугольных треугольников: «Если две стороны и высота, проведённая к третьей стороне одного тупоугольного треугольника, соответственно равны двум сторонам и высоте, проведённой к третьей стороне другого тупоугольного треугольника, то такие треугольники равны». Не ошибается ли Саша?

Задача 47. (Григорий Гальперин)
Квантик выписал в порядке возрастания все 9-значные числа, в записи каждого из которых участвуют по одному разу все ненулевые цифры от 1 до 9: начиная от 123456789 и кончая 987654321. Затем Квантик выписал все положительные разности соседних чисел этой цепочки и нашёл общую сумму этих разностей. Докажите, что в итоге Квантик получил одно из чисел исходной цепочки 9-значных чисел. Какое именно?

Задача 48. (Николай Авилов)
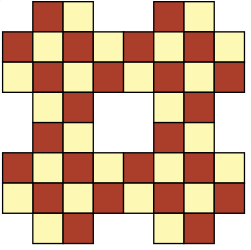
Проложите замкнутый маршрут шахматного коня, проходящий по одному разу по всем клеткам изображённой на рисунке фигурной доски.

Задача 49. (Андрей Аржанцев)
Факториалом натурального числа n называется произведение всех целых чисел от 1 до n, то есть 1·2·…·n. Обозначение: n! (читается «эн факториал»). Существует ли такое n, что n! равно
а) произведению двух факториалов различных натуральных чисел, больших 1;
б) произведению 2019 факториалов нату-ральных чисел, которые все различны?

Задача 50. (Александр Ковальджи)
У каждого из 100 друзей есть ровно 10 интересов, и у каждых двоих из них ровно 1 общий интерес. Докажите, что у всех 100 друзей есть общий интерес.

IX тур
Задача 41. (Константин Кноп)
Вставьте в пустые клетки различные числа от 1 до 10 так, чтобы получилось верное равенство: □ + □×□ + □×□×□ + □×□×□×□ = 5167.

Задача 42. (Марк Пименов, 5 кл.)
На расстоянии 9 км друг от друга стоят шарикометатель и игломёт. Шарикометатель выпускает по воздушному шарику каждую минуту. Каждый шарик летит по прямой со скоростью 2 ⅓ км/мин в направлении игломёта. Как только шарик оказывается в зоне поражения – на расстоянии не более 5 км от игломёта, – игломёт мгновенно его подстреливает. Правда, игломёту после каждого выстрела нужно 1 ⅔ минуты, чтобы перезарядиться. Если в зоне поражения несколько шариков, лопается только ближайший к игломёту. Какой по счёту шарик всё-таки долетит до игломёта?

Задача 43. (Егор Бакаев)
Ребята два дня решали задачи. В первый день Петя решил задач в 2 раза меньше Васи и в 3 раза меньше Маши. Во второй день Маша решила задач в 2 раза меньше Пети и в 1,5 раза меньше Васи. Может ли быть так, что Вася решил больше задач, чем каждый из других ребят?

Задача 44. (Михаил Евдокимов)
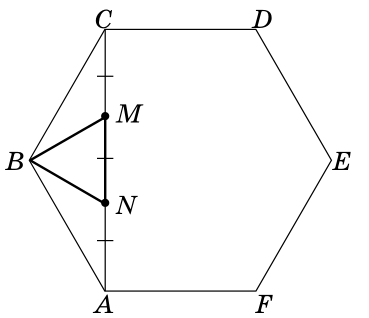
Точки M и N делят диагональ AC правильного шестиугольника ABCDEF на три равные части. Докажите, что треугольник MBN равносторонний.

Задача 45. (Юрий Чеканов)
В шахматной доске 8×8 вырезали центральный квадрат размером 2×2 клетки.
а) Какое наибольшее число ферзей, не бьющих друг друга, можно поставить на получившуюся доску? Приведите пример расстановки и докажите, что большее число ферзей расставить нельзя.
б) Сколько всего таких расстановок? Нарисуйте их все и докажите, что других нет.
(Ферзи бьют друг друга, если они находятся на одной клетчатой линии – вертикали, горизонтали или диагонали – и в этой линии нет вырезанных клеток.)

VIII тур
Задача 36. (Григорий Гальперин)
Ствол одного дерева распилили на несколько частей, а потом ствол другого дерева распилили за вдвое большее время на другое число частей. Докажите, что во втором случае число частей нечётно. (На каждый распил тратили одно и то же время.)

Задача 37. (Михаил Малкин)
Можно ли из 1000 чисел 1, ½, 1/3, …, 1/1000 выбрать 8 чисел и записать их в ряд так, чтобы разности между соседними числами были одинаковы?

Задача 38. (Юрий Маркелов)
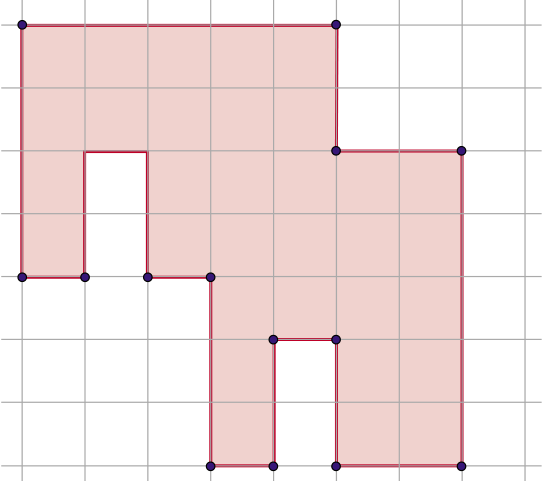
Разделите данную фигуру на две равные части.

Задача 39. (Константин Кноп)
У Кости было 26 одинаковых на вид монет, среди них 21 – настоящие, которые весят поровну, и 5 – фальшивые, которые тоже весят поровну, но несколько легче. Все вместе они весили 421 г. Костя потерял 5 монет, и теперь оставшиеся весят только 340 г. Сколько весит настоящая монета?

Задача 40. (Александр Грибалко)
Костяшка домино имеет вид прямоугольника 1×2, разделённого на два квадратика 1×1, на каждом квадратике выбито от 0 до 6 очков. В полном наборе домино 28 неповторяющихся костяшек. Можно ли уложить их все в коробку 4×7 в два слоя так, чтобы каждые два квадратика, находящиеся на одном и том же месте в разных слоях, содержали одинаковое число очков?

VII тур
Задача 31. (Павел Кожевников)
Можно ли расставить по окружности числа 1, 2, 3, … , 100 так, чтобы любые два соседних числа различались не более чем на 2?

Задача 32. (Михаил Евдокимов)
Клетчатый квадрат 7×7 разрезали по линиям сетки на различные прямоугольники. Какое наибольшее число прямоугольников могло получиться?

Задача 33. (Михаил Евдокимов)
Каждый из кандидатов в мэры либо лжец (всегда лжёт), либо правдолюб (всегда говорит правду), и все кандидаты знают, кто есть кто. В начале дебатов каждый из 25 кандидатов заявил: «Среди остальных присутствующих кандидатов лжецов больше, чем правдолюбов». После того как подошёл опоздавший 26-й кандидат, каждый из кандидатов повторил своё заявление. Кем является опоздавший: лжецом или правдолюбом?

Задача 34.
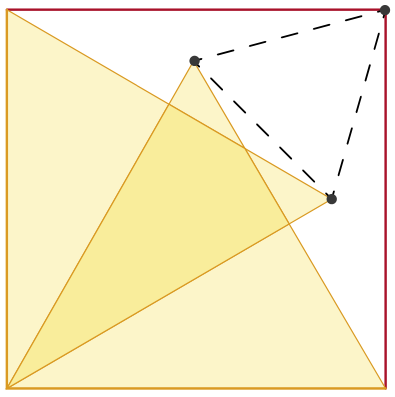
Два жёлтых равносторонних треугольника расположены в квадрате, как показано на рисунке. Докажите, что три выделенные точки образуют равносторонний треугольник.

Задача 35. (Александр Ковальджи)
По кругу выкладывают 30 одинаковых на вид таблеток, из них 20 хороших и 10 плохих. Два мудреца по очереди берут по одной таблетке. Первый мудрец будет знать, где лежат плохие таблетки, а второй – нет. Мудрецы хотят до выкладывания таблеток договориться, как после каждого хода первого второй найдёт хорошую таблетку. После 20 ходов на столе должны остаться 10 плохих таблеток. Предложите алгоритм действий для мудрецов. (Беря таблетки, мудрецы не общаются и не подают никаких знаков. Каждый видит, какую таблетку взял партнёр.)

VI тур
Задача 26.
Среди 12 человек нет людей одного роста. Они выстроились в круг, после чего те, кто выше обоих своих соседей, подняли левую руку, а кто ниже обоих своих соседей – правую. Могло ли случиться, что а) никто не поднял руки; б) все подняли руку?

Задача 27. (Игорь Акулич)
Можно ли на некоторые клетки шахматной доски 8×8 поставить по фишке так, чтобы количества фишек в любых двух соседних вертикалях и в любых двух соседних горизонталях были ненулевыми и отличались а) в 5 раз; б) в 6 раз?

Задача 28. (Григорий Гальперин)
31 декабря 19 человек справляли Новый год. Каждому гостю дали две карточки, маленькую и большую, и попросили написать на маленькой карточке свой возраст (число полных лет), а на большой – свой год рождения. После этого все карточки смешали и произвольно разделили на две группы. В первой группе сумма чисел поделилась на 19. Обязательно ли тогда и во второй группе сумма чисел поделилась на 19?

Задача 29. (Николай Авилов)
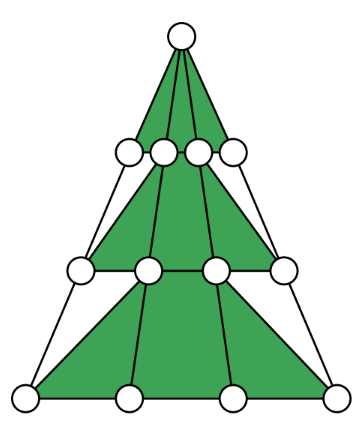
Ёлочка украшена тремя горизонтальными гирляндами и четырьмя гирляндами, спускающимися с вершины вниз. Во всех гирляндах по четыре шарика. Впишите в шарики все целые числа от 1 до 13 (в каждый шарик по одному числу) так, чтобы сумма четырёх чисел в каждой из семи гирлянд была одной и той же.

Задача 30. (Егор Бакаев)
Можно ли раскрасить все точки бесконечной плоскости в а) 3; б) 4 цвета так, чтобы все цвета присутствовали, но нельзя было провести окружность, на которой есть точки всех цветов? (Кисточка, которой красится плоскость, настолько тонкая, что можно любую точку покрасить в любой цвет, не запачкав никакие другие точки.)

V тур
Задача 21. (Сергей Костин)
Из спичек сложен равносторонний треугольник со стороной 2 (см. рисунок). Два игрока по очереди убирают по одной спичке. Проигрывает игрок, после хода которого не останется ни одного треугольника, составленного из трёх спичек. Кто может обеспечить себе победу – начинающий или его противник – и как ему играть?


Задача 22. (Михаил Энгельгардт)
Придумайте какое-нибудь число, квадрат которого состоит только из цифр 1, 2, 3 и все эти цифры присутствуют.

Задача 23. (Сергей Костин)
Сад в форме квадрата 6×6 окружён невысоким забором. Садовник хочет посадить в саду яблони (не более одной в каждой клетке квадрата) так, чтобы ни одна яблоня не была в тени. Яблоня находится в тени, если с четырёх сторон от неё (в четырёх соседних по стороне клетках сада) растёт по яблоне. Какое наибольшее число яблонь может посадить садовник? Приведите пример и докажите, что больше яблонь посадить нельзя.

Задача 24. (Лев Емельянов)
Петя и Вася купили по конструктору «Собери тетраэдр». В конструкторе 4 треугольника – будущие грани тетраэдра. По дороге Петя потерял один треугольник. Заметив это дома, он побежал с остатками своего конструктора к Васе. Сравнивая детали, они обнаружили, что среди четырёх Васиных треугольников есть три таких же, как у Пети. «Отлично, теперь я знаю, какой треугольник я потерял!» – воскликнул Петя. «Вот только почему цены конструкторов отличаются?» – задумался он. А могло ли быть так, что у ребят конструкторы отличались одним треугольником, но из каждого можно было собрать свой тетраэдр?

Задача 25. (Павел Кожевников)
Найдутся ли 100 различных натуральных чисел, никакие два из которых не имеют общих множителей, больших 1, но среднее арифметическое любых нескольких из них – целое?

IV тур
Задача 16. (Ольга Зайцева-Иврии)
У Андрея в ящике вперемешку лежат носки: целые – их 60%, и с дырками – их 40%. Когда Андрей достал 4 носка, процент оставшихся носков с дырками в ящике возрос до 50%. Сколько носков в ящике могло быть первоначально? Найдите все ответы и докажите, что других нет.

Задача 17. (Александр Ковальджи)
Можно ли рассадить за круглым столом через равные промежутки между людьми 20 молчунов и несколько болтунов так, чтобы напротив каждого молчуна сидел болтун и чтобы никакие два болтуна не сидели рядом?

Задача 18. (Юрий Маркелов)
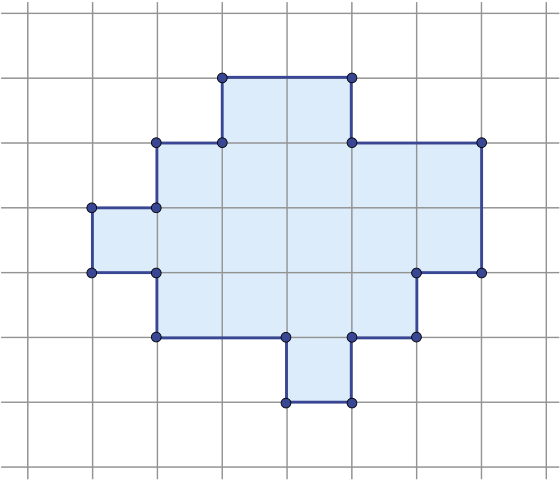
Разделите фигуру на рисунке на две равные части двумя разными способами.

Задача 19. (Игорь Акулич)
Можно ли представить в виде суммы нескольких (не менее двух) последовательных нечётных натуральных чисел: а) 2017; б) 2018; в) 2019?

Задача 20. (Егор Бакаев)
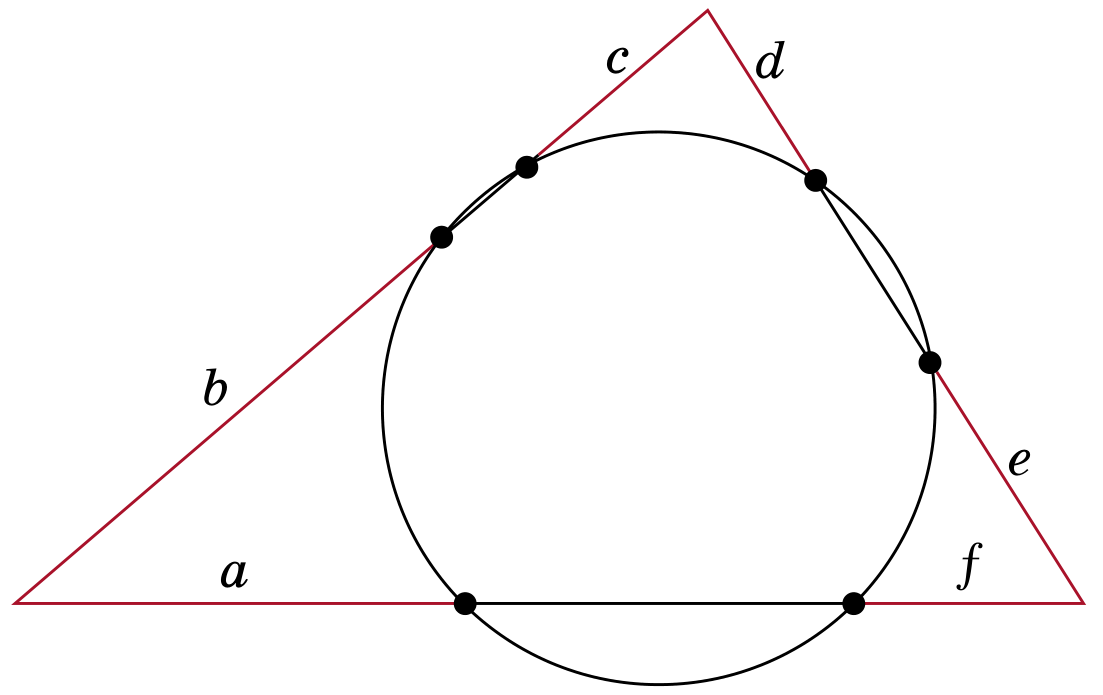
Окружность пересекает стороны треугольника в шести точках (см. рисунок).
а) Докажите, что если a = b и c = d, то e = f.
б) Докажите, что если b = c и d = e, то f = a.

III тур
Задача 11. (Юрий Маркелов)
Электронные часы показывают часы и минуты. Вася подошёл к часам и заметил, что сейчас на них палиндром – время выглядит как AB:BA. Он решил подождать, когда это повторится, но, просидев 4 часа, так и не увидел второго палиндрома. А сколько ему ещё осталось ждать?

Задача 12. (Владимир Расторгуев)
На прямой лежат точки A, C, D, B именно в этом порядке. Построены равнобедренные прямоугольные треугольники AGD, BHD с гипотенузами AD, BD – по одну сторону от прямой, и треугольники AEC, BFC с гипотенузами AC, BC – по другую сторону от прямой. Докажите, что прямые EH и GF перпендикулярны.

Задача 13. (Иван Митрофанов)
Докажите, что любое целое число, не меньшее 12, можно записать как сумму двух составных чисел.

Задача 14. (Юрий Маркелов и Соня Голованова)
(продолжение задачи 1).
а) Можно ли зачеркнуть 8 клеток в клетчатом квадрате 6×6 так, чтобы не было 5 незачёркнутых клеточек подряд ни по горизонтали, ни по вертикали, ни по диагонали.
б) А можно ли так зачеркнуть всего 7 клеток?

Задача 15. (Ольга Зайцева-Иврии)
На N карточках Лена написала числа от 1 до N (по одному на карточке) синим фломастером, а на N других карточках – эти же числа красным фломастером. Затем она перемешала отдельно карточки с синим цветом, отдельно – с красным и положила стопку красных карточек на стопку синих. В получившейся колоде для каждой пары карточек с одним и тем же числом Лена записала на бумажку, сколько между ними лежит других карточек. Затем она сложила все записанные на бумажку числа. Какой результат могла получить Лена?

II тур
Задача 6. (Сергей Дворянинов)
Найдите наименьшее такое натуральное число, что и в его записи, и в записи удвоенного числа встречаются все десять цифр от 0 до 9.

Задача 7. (Александр Грибалко)
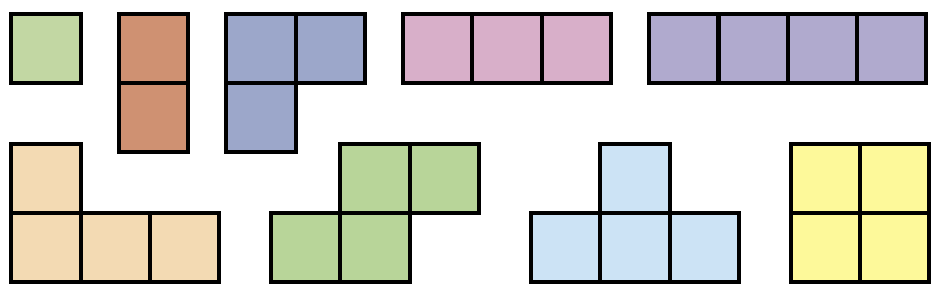
В наборе присутствуют по одному разу всевозможные фигурки из одной, двух, трёх и четырёх клеток (см. рисунок).
а) Выложите их «по клеточкам» на доску 8×8 так, чтобы никакие две фигурки не перекрывались и не касались даже углами (фигурки разрешается переворачивать).
б) Можно ли это сделать, если дополнительно требуется, чтобы на доске поместилась ещё одна одноклеточная фигурка, не имеющая общих точек с уже выложенными?

Задача 8. (Евгений Смирнов)
На планете Шелезяка в году 12 месяцев, во всех месяцах поровну дней. Её юному жителю Плексу меньше 100 лет. Возраст Плекса в годах представляется несократимой дробью, в числителе и знаменателе которой – квадраты целых чисел. А его возраст в месяцах – куб целого числа. Сколько Плексу лет и месяцев?

Задача 9. (Игорь Акулич)
На шахматной доске 8×8 расставили 7 слонов так, чтобы никакие два не били друг друга. Обязательно ли после этого удастся переставить каждого слона на другое поле ходом коня так, чтобы в новой расстановке никакие два слона по-прежнему не били друг друга?

Задача 10. (Егор Бакаев и Павел Живцов)
а) В зале музея стоят по кругу 5 одинаковых шкатулок. Каждый вечер начальник охраны запирает две шкатулки по своему выбору, положив в одну из них бесценный алмаз. Подкупленный работник музея видит действия начальника и хочет оставить взломщику подсказку, где алмаз. Для этого он открывает крышки ровно у двух незапертых шкатулок, а остальные не трогает. Как ему заранее договориться со взломщиком, чтобы тот, придя ночью в музей и увидев, у каких двух шкатулок открыты крышки, сразу понял, где лежит алмаз?
б) Та же задача, но в зале стоят по кругу 33 шкатулки, начальник запирает 16 шкатулок, положив в одну алмаз; взломщик должен понять, где алмаз, по двум шкатулкам, у которых открыты крышки.

I тур
Задача 1. (Соня Голованова и Юрий Маркелов)
В клетчатом квадрате 6×6 можно зачеркнуть 9 клеток так, чтобы не было 5 незачёркнутых клеточек подряд ни по горизонтали, ни по вертикали (см. рисунок). А можно ли зачеркнуть всего
а) 8 клеток;
б) 7 клеток;
в) 6 клеток
так, чтобы выполнялось то же условие?

Задача 2. (Евгений Братцев)
У входа в парк развлечений висит электронное табло, показывающее время (часы и минуты). Когда табло показало 9:00, в парке открылись шесть аттракционов и работали до вечера по 1, 2, 3, 4, 5 и 6 минут соответственно с минутным перерывом. Когда Олег пришёл днём в парк, ни один аттракцион не работал. Какое время показывало электронное табло в этот момент?

Задача 3.
Квантик написал 100 различных натуральных чисел, а Ноутик написал число, делящееся на каждое из них. Докажите, что число Ноутика хотя бы в 100 раз больше самого маленького числа у Квантика.

Задача 4. (Сергей Костин)
Разрежьте квадрат 5×5, в центре которого вырезано отверстие 1×1, на три фигуры с равными периметрами и равными площадями.


Задача 5. (Игорь Акулич)
а) Квантик и Ноутик показывают такой фокус. Зритель задумывает любые шесть разных целых чисел от 1 до 125 и сообщает их только Ноутику. После этого Ноутик называет Квантику какие-то пять из них, и Квантик угадывает шестое задуманное зрителем число. Предложите способ, как могли бы действовать Квантик и Ноутик, чтобы фокус всегда удавался.
б) Сумеют ли фокусники добиться успеха, если зритель сам указывает Ноутику, какие пять из шести задуманных им чисел Ноутик должен назвать Квантику?


