Математический конкурс 2019/20 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (Григорий Гальперин)
На бумаге начертили 130 четырёхугольников. Каждый четырёхугольник – или квадрат, или прямоугольник, или параллелограмм, или ромб, или трапеция. Из них 30 – квадраты, 80 – прямоугольники, 65 – ромбы, и 120 – параллелограммы. Сколько всего трапеций было начерчено? (Напомним, что у трапеции две стороны параллельны, а две – нет.)

Задача 57. (Александр Грибалко)
По кругу лежат 4 одинаковые с виду монеты. Две из них фальшивые – они весят 9 г и 11 г, а две настоящие – весят по 10 г каждая. Известно, что фальшивые монеты соседние. За какое наименьшее число взвешиваний на чашечных весах без гирь можно гарантированно определить вес каждой монеты? (Весы лишь показывают, равны ли чаши по весу, и если нет, то какая тяжелее.)

Задача 58. (Борис Кордемский)
У Квантика на даче есть участок треугольной формы. Он решил застелить его газоном. Зная третий признак равенства треугольников, он измерил три стороны участка и заказал треугольный газон с такими сторонами. Но когда заказ был доставлен, Квантик не смог наложить газон на свой участок, хотя длины сторон были в точности как в заказе.
а) Как такое могло быть?
б) Как Квантику исправить ситуацию, разрезав газон не более чем на три части?

Задача 59. (Михаил Евдокимов)
Вася расставил по кругу в некотором порядке числа 1, 2, 3, …, 15 и целое число x (не обязательно положительное). Оказалось, что сумма любых двух соседних чисел – квадрат целого числа.
а) Найдите хотя бы одно такое x и нарисуйте соответствующую расстановку.
б) Найдётся ли другое подходящее x?

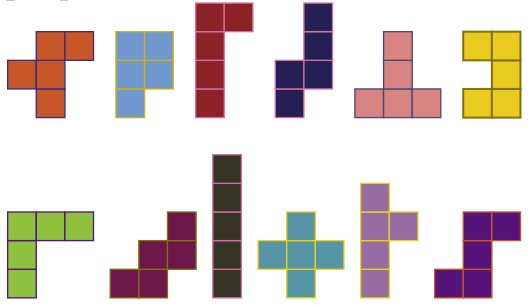
Задача 60. (Сергей Костин)
Любую ли фигуру пентамино (см. рисунок) можно дополнить доминошками до клетчатого квадрата без дырок и перекрытий?

XI тур
Задача 51. (Александр Домашенко)
В числовом ребусе
Т×О×П×О×Л×Ь=Т×Ю×Л×Ь×П×А×Н
замените буквы ненулевыми цифрами так, чтобы число ТОПОЛЬ получилось как можно бо́льшим. (Одинаковые буквы заменяйте одинаковыми цифрами, разные – разными.) Не забудьте обосновать ответ.

Задача 52. (Михаил Евдокимов)
Расставьте на шахматной доске несколько белых и чёрных коней так, чтобы каждый белый конь бил ровно четырёх чёрных, а каждый чёрный – ровно четырёх белых.

Задача 53. (Александр Домашенко)
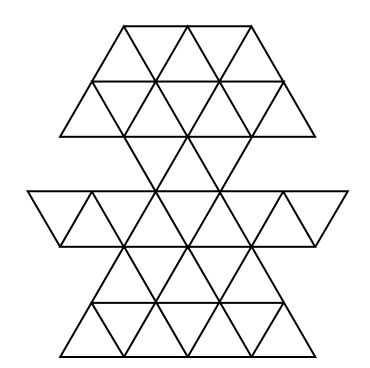
Аня вырезала куклу из бумаги в треугольную сетку. Юра утверждает, что эту фигурку можно свернуть в треугольную пирамидку без просветов и наложений. Прав ли он?

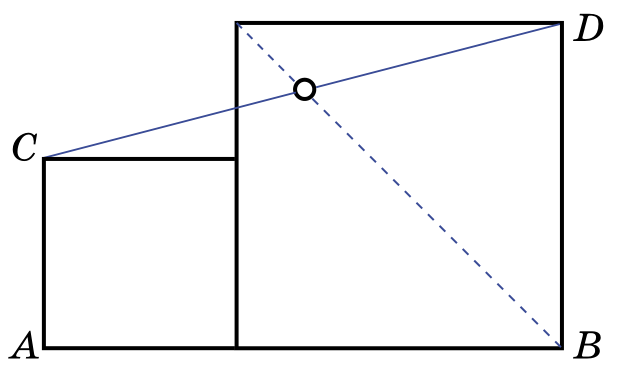
Задача 54. (Михаил Евдокимов)
На отрезке AB построены два различных прилегающих друг к другу квадрата (см. рисунок). Докажите, что диагональ большого квадрата делит отрезок CD пополам.

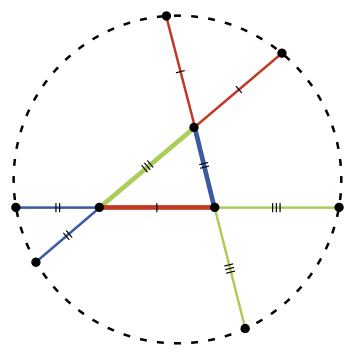
Задача 55. (Алексей Воропаев)
Петя стреляет по мишени. Табло показывает отношение числа попаданий к числу сделанных выстрелов (до начала стрельбы табло не горит). В какой-то момент число на табло было меньше чем q. Через некоторое время это число стало больше, чем q. Для каких q от 0 до 1 отсюда следует, что в какой-то момент доля попаданий была ровно q?

X тур
Задача 46. (Мария Ахмеджанова)
Квантик получил по почте кубическую посылку, запечатанную со всех сторон. Он хочет открыть коробку, разрезав её по рёбрам на две части, но так, чтобы у любой грани было разрезано не более двух рёбер. Удастся ли ему это?

Задача 47. (Михаил Евдокимов)
Два лифта едут вниз с одинаковой скоростью с 95-го этажа офисного небоскрёба. Второй лифт стартовал через 45 секунд после первого. На этажах с номерами, делящимися на 2 или 3, стоит по сотруднику (остальные этажи пустые). Всем нужно на первый этаж. Лифт, приехавший к сотруднику первым, останавливается на 10 секунд, чтобы его забрать (другой лифт проезжает мимо). Какой лифт раньше попадёт на первый этаж?

Задача 48. (Михаил Евдокимов)
У фокусника есть две копии «хитрой» клетчатой фигуры. Зритель называет любое целое число N от 2 до 100, и фокусник разрезает первую копию на N клетчатых частей, из которых можно сложить квадрат, а вторую копию – на N клетчатых частей, из которых нельзя сложить квадрат. Приведите пример «хитрой» фигуры и объясните, как разрезать её в каждом из случаев, чтобы фокус удавался. (Все части должны использоваться; наложения частей и дырки не допускаются.)

Задача 49. (Сергей Костин)
Каких семизначных натуральных чисел больше: у которых произведение цифр равно 1024, или у которых произведение цифр равно 2048?

Задача 50. (Джон Конвей)
Каждую сторону произвольного треугольника продлили в обе стороны так, как показано на рисунке. Докажите, что полученные 6 точек лежат на одной окружности.

IX тур
Задача 41. (Михаил Евдокимов)
Перед игроком стоят в ряд 3 шкатулки, в одной из которых лежит приз. К шкатулкам прикреплены записки с утверждениями, как на рисунке. Известно, что ровно одно из утверждений истинно. Какую шкатулку нужно открыть, чтобы получить приз?

Задача 42. (Сергей Дворянинов)
Толя Втулкин отметил на прямой три точки и заметил, что всевозможных отрезков с концами в этих точках оказалось 3, а всевозможных лучей с началами в этих точках – 6, в два раза больше.
«Интересно, – подумал Толя, – а можно ли отметить столько точек, чтобы получилось наоборот: число всевозможных лучей с началами в этих точках было бы в два раза меньше количества всевозможных отрезков с концами в этих точках?»
Ответьте на вопрос Толи.

Задача 43. (Михаил Евдокимов)
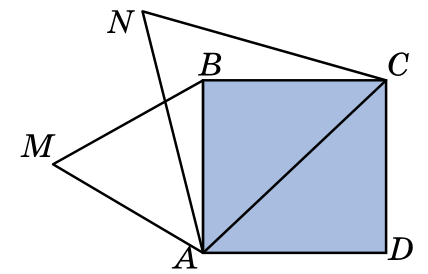
На диагонали и стороне единичного квадрата ABCD построены правильные треугольники AMB и ANC так, как показано на рисунке. Чему равно расстояние MN?

Задача 44. (Игорь Акулич и Максим Прасолов)
Число 1210 обладает таким свойством: каждая его цифра, кроме последней, показывает, сколько раз в нём встречается следующая цифра. А именно: «12» означает, что в числе одна двойка, «21» – что в числе две единицы, «10» – что в числе один ноль. Существует ли число с таким же свойством, большее миллиарда?

Задача 45. (Сергей Костин)
Можно ли записать в клетках фигуры F натуральные числа так, чтобы сумма чисел в любом горизонтальном прямоугольнике 1×3, целиком лежащем внутри фигуры, равнялась 10, а сумма чисел в любом вертикальном прямоугольнике 3×1, целиком лежащем внутри фигуры, равнялась 11, если фигура F – это
а) квадрат 5 × 5;
б) квадрат 5 × 5, у которого удалили центральную клетку?

VIII тур
Задача 36. (Григорий Гальперин)
Петя решал задачу из книги: «В Канаде __ процентов населения говорит по-английски, а __ процентов – по-французски (на других языках в Канаде не говорят). Какой процент населения Канады говорит и по-английски, и по-французски?». (Числа из книги мы заменили пропусками.) «Какая лёгкая задача! – сказал он. – Надо просто вычесть из первого числа второе, вот и всё решение!» Петя посмотрел ответы в конце книги и убедился, что его ответ правильный. Какой процент населения Канады говорит по-французски, по мнению этой книги?

Задача 37. (Александр Перепечко)
Когда родился Квантик, его старшему брату было x месяцев. Число x равно наименьшему общему кратному всех чисел от 1 до 9, кроме одного, а также равно произведению трёх последовательных чисел. Сколько полных лет старшему брату, если Квантику сейчас 100 месяцев?

Задача 38. (Владимир Расторгуев)
Клетчатые квадраты 12×12 и 5×5 разрежьте (один или оба) по линиям сетки так, чтобы всего получилось пять кусков и из этих пяти кусков можно было сложить квадрат 13×13.

Задача 39. (Сергей Дворянинов)
Положительные числа x и y таковы, что в неравенстве ниже левая дробь больше правой. Что больше: x или y?
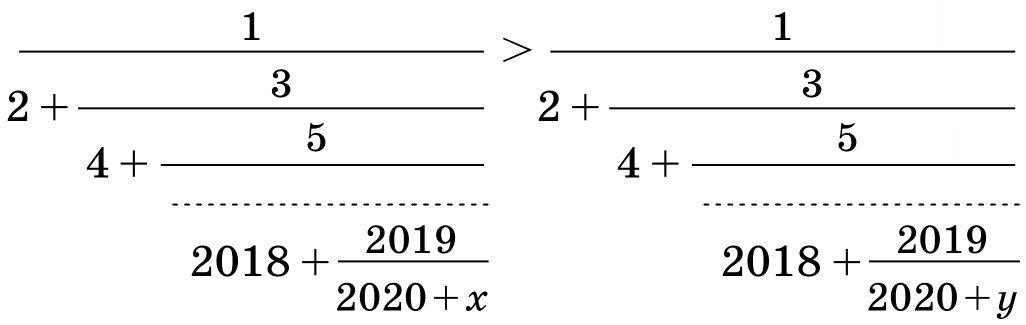

Задача 40. (Борис Френкин)
В окружность вписан 1000-угольник, его вершины покрашены поочерёдно в красный и синий цвет. Каково наибольшее возможное количество красных вершин, углы при которых меньше 179°?

VII тур
Задача 31. (Инесса Раскина)
Мимо пассажира «Ласточки», едущей с постоянной скоростью, встречный «Сапсан» пронёсся за 3 секунды, а попутный «Сапсан» – за 7 секунд. Длины и скорости «Сапсанов» были одинаковы. За сколько секунд этот пассажир проедет мимо такого же, но стоящего «Сапсана»?

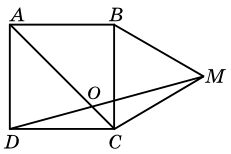
Задача 32. (Михаил Евдокимов)
На стороне BC квадрата ABCD во внешнюю часть построен равносторонний треугольник BMC. Отрезки AC и MD пересекаются в точке O. Докажите, что OA = OM.

Задача 33. (Сергей Дориченко)
Три разбойника украли пять алмазов (возможно, разного веса) и решили разделить их между собой поровну по весу, не распиливая на куски. Они отмерили треть, но остальные алмазы нельзя было разделить на две равные части. Докажите, что разбойникам не удастся поделить алмазы, даже если они смогут отмерить треть по-другому.

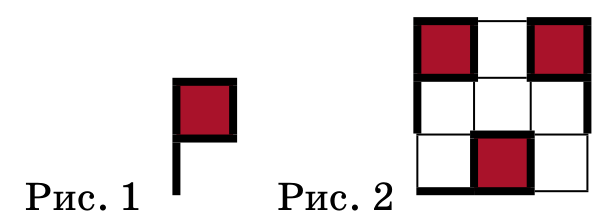
Задача 34. (Сергей Костин)
Какое наибольшее количество флажков, изображённых на рисунке 1, можно разместить в квадрате а) 8×8; б) 14×14? Флажок должен располагаться по линиям сетки. Никакие два флажка не должны иметь ни одной общей точки. В качестве примера на рисунке 2 показано, как в квадрате 3×3 можно разместить три флажка.

Задача 35. (Игорь Акулич)
В гирлянде n лампочек и n кнопок с номерами. По инструкции, 1-ю кнопку надо соединить с одной лампочкой, 2-ю – с двумя, 3-ю – с тремя, и т. д., но с какими именно лампочками соединяется каждая кнопка, решает пользователь. Сначала все лампочки погашены. Нажатие на любую кнопку меняет состояние всех соединённых с ней лампочек на противоположное (горящие лампочки гаснут, не горящие – зажигаются).
Коля уверен, что можно так соединить кнопки с лампочками, чтобы, нажав нужные кнопки, можно было получить любую комбинацию горящих и не горящих лампочек. Петя же считает, что любую такую комбинацию можно получить, как ни соединяй лампочки и кнопки – лишь бы по инструкции.
а) При каких n прав Коля?
б) При каких n прав Петя?

VI тур
Задача 26. (по мотивам задачи Мартина Гарднера)
Число 1210 автобиографичное: его первая цифра показывает, сколько в нём нулей, вторая – сколько единиц, третья – сколько двоек, а четвёртая – сколько троек. Найдите следующее автобиографичное целое число.

Задача 27. (Александр Перепечко)
У барона Мюнхгаузена есть волшебный кубик, в котором две грани – синие, две – красные и две – зелёные. Если поставить этот кубик на любую грань и запомнить, где какой цвет, то на какую бы другую грань потом ни ставить кубик, не удастся повторить такое же расположение цветов. Может ли так быть?

Задача 28. (Николай Авилов)
Снежинка «соткана» из семи окружностей, на них расположены кружки, по 6 на каждой окружности. В кружках расставлены числа от 1 до 19 (см. рисунок). Переставьте 6 чисел так, чтобы на каждой окружности сумма чисел была одной и той же.
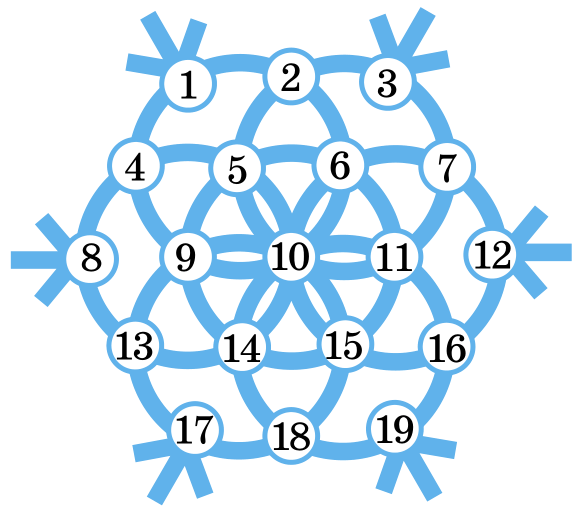

Задача 29. (Александр Блинков и Антон Акимов)
Ноутику и Квантику дали задание: нарисовать какой-нибудь четырёхугольник ABCD, в котором стороны AD и BC параллельны и AN = CM, где M – середина AB, а N – середина CD. Ноутик нарисовал параллелограмм, а Квантик – даже два разных четырёхугольника, но оба не параллелограммы. Могло ли такое быть, если все примеры верные и в каждом AD = 14, AN = CM = 5, а расстояние между AD и BC равно 8?

Задача 30. (Сергей Костин)
В каждой клетке таблицы 7×7 стоит минус. За ход можно в любом квадрате 2×2 поменять все знаки на противоположные. Какое наибольшее количество плюсов можно получить в таблице с помощью таких ходов?

V тур
Задача 21. (Александр Перепечко)
Барон Мюнхгаузен огородил свои владения забором в форме шестиугольника. Он утверждает, что каждый внутренний угол этого шестиугольника либо меньше 10°, либо больше 350°. Может ли барон быть прав?

Задача 22. (Павел Кожевников)
Вася написал на листке 10 цифр (среди них могут быть равные) так, чтобы сумма любых трёх написанных цифр не превосходила 14. Какова наибольшая возможная сумма всех 10 цифр? (Приведите пример и докажите, что большую сумму получить нельзя.)

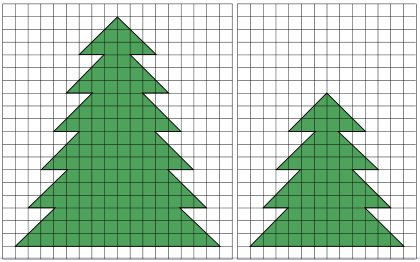
Задача 23. (Николай Авилов)
Ёлочку на рисунке слева разрежьте на четыре части и сложите из них две одинаковые ёлочки, как на рисунке справа.

Задача 24. (Григорий Мерзон)
Вычислите сумму
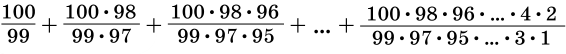

Задача 25. (Николай Чернятьев)
Квантик и Ноутик по очереди закрашивают клетки на доске 8×8, по одной клетке за ход, начинает Квантик. Первый ход можно сделать куда угодно. Каждый следующий ход должен быть таким, что новая клетка граничит по стороне ровно с одной закрашенной клеткой. Кто не может сделать ход, проиграл. Кто может обеспечить себе победу?

IV тур
Задача 16. (Александр Хачатурян и Татьяна Казицына)
Саша придумал шифр: заменил несколько букв однозначными или двузначными числами, используя только цифры 1 и 2 (разные буквы он заменял разными числами, а одинаковые – одинаковыми). Слово КРОЛИК превратилось в число 1212111212. Слово КРОКОДИЛ тоже превратилось в число. В какое?

Задача 17. (Михаил Евдокимов)
Найдите наименьшее семизначное число, делящееся на 17, в котором все цифры разные.

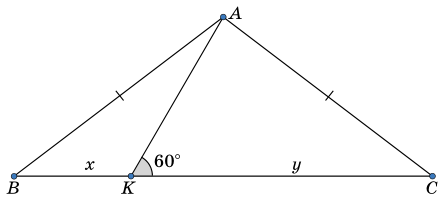
Задача 18.
Точка K делит основание BC равнобедренного треугольника BAC на отрезки длины x и y, как показано на рисунке. Найдите длину AК, если угол AКC равен 60°.

Задача 19.
Квантик и Ноутик хотят показать такой фокус. Зритель задумывает два натуральных числа, различающихся на 1, и сообщает одно Квантику, а другое – Ноутику. После этого Квантик показывает Ноутику чёрную или белую карточку, и Ноутик сразу угадывает число Квантика. Помогите Квантику и Ноутику договориться о своих действиях, чтобы фокус всегда удавался.

Задача 20. (Владимир Расторгуев)
Разрежьте шестиугольник на рисунке на две равные части.

III тур
Задача 11. (Александр Перепечко)
Семь камней весом 1, 2, 3, 4, 5, 6 и 7 тонн можно перевезти в нескольких грузовиках одинаковой грузоподъёмности. Хватит ли для перевозки четырёх таких грузовиков?

Задача 12. (Борис Френкин)
Петя и Вася тренируются на кольцевом велотреке: одновременно стартовали из одной и той же точки и едут с постоянными скоростями. Петя едет быстрее Васи. Когда Петя прошёл 16 кругов, он встретил в точке старта Васю. А когда Вася прошёл 16 кругов, он встретил в точке старта Петю. Верно ли, что Вася после каждого круга встречал в точке старта Петю?

Задача 13. (Александр Грибалко)
У Саши есть два клетчатых квадрата 7×7. Ему нужно разрезать их по линиям сетки на части так, чтобы частей получилось не более пяти и их можно было уложить в один слой в коробку 10×10. Есть ли способ выполнить это задание?

Задача 14. (Алексей Воропаев)
Квантик и Ноутик загадали по натуральному числу и сказали их Серёже. Серёжа в ответ назвал число 2020 и сказал, что это либо сумма, либо произведение услышанных им чисел. Ноутик подумал и сказал, что не знает, какое число загадал Квантик. Квантик услышал это, но всё равно не смог узнать, какое число загадал Ноутик. Какое число загадал Квантик?

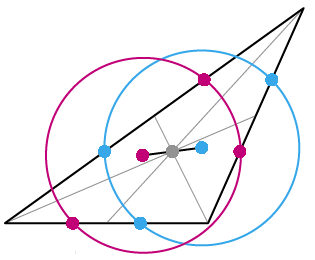
Задача 15. (ученик 4 класса Петя Ким)
На каждой из сторон треугольника ABC выбраны красная и синяя точки так, что красная точка делит сторону в отношении 2 : 1, а синяя – в отношении 1 : 2 (если обходить треугольник по часовой стрелке). Через красные точки провели окружность, и через синие – тоже. Докажите, что отрезок, соединяющий центры этих окружностей, проходит через точку пересечения медиан треугольника ABC.

II тур
Задача 6. (Григорий Гальперин)
Каких чисел, все цифры которых различны, больше: девятизначных или десятизначных?

Задача 7. (Григорий Гальперин)
У Квантика есть две квадратные шоколадки, первая – размером 10×10, вторая – размером 11×11. Чтобы разломать первую шоколадку на дольки 1×1, Квантику требуется 1 минута и 39 секунд. Какое время ему потребуется, чтобы разломать на дольки 1×1 вторую шоколадку? На каждый разлом Квантик тратит одно и то же время и за раз ломает какой-то один из имеющихся кусков на две части.

Задача 8. (Игорь Акулич)
Барон Мюнхгаузен рассказывал:
– Я сумел разрезать произвольный треугольник на две части, а потом каждую из них разрезал на 7 равных частей.
Могут ли слова барона быть правдой?

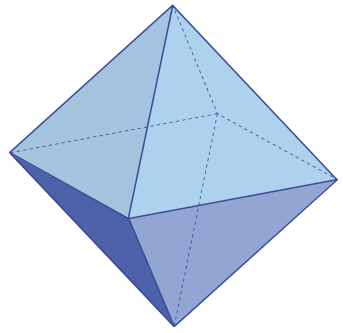
Задача 9. (Александр Перепечко)
Многогранник, изображённый на рисунке, называется октаэдром; у него 6 вершин, 8 треугольных граней и 12 рёбер. В каждой вершине октаэдра поместили лампочку и зажгли одну из них. Далее, за ход можно выбрать любую грань и изменить состояние (потушить, если горит, и зажечь, если не горит) всех лампочек на ней. Можно ли за несколько ходов зажечь все лампочки?

Задача 10. (Игорь Акулич)
Возьмём любое натуральное число, например, 2019. Составим второе число, которое показывает, сколько и каких цифр (в порядке возрастания) содержит исходное число. Получится 10111219, что означает «один нуль, одна единица, одна двойка и одна девятка». На основе второго числа по тому же принципу образуем третье число 10511219, потом – четвёртое 1041121519, и т. д.
а) Квантик убеждён, что с какого бы числа ни начать, в получившейся последовательности какое-то число непременно встретится дважды. Ноутик считает, что не обязательно – возможна последовательность, в которой все числа различны. Кто прав?
б) Могут ли в такой последовательности встретиться два одинаковых числа подряд?

I тур
Задача 1. (Сергей Дворянинов)
Однажды Толик Втулкин должен был найти произведение двух чётных трёхзначных чисел. Он спешил и в записи одного числа пропустил наименьшую цифру, а в записи другого – наибольшую. В итоге он получил 323. Какие числа должен был перемножить Толик?

Задача 2. (Павел Кожевников)
Разрежьте клетчатую доску 12×12 на четыре одинаковых клетчатых многоугольника так, чтобы никакой клетчатый квадрат 2×2 не попал целиком ни в какой многоугольник.

Задача 3. (Павел Кожевников)
Вася хочет выбрать из набора 1, 2, 3, … , 50 как можно больше чисел так, чтобы любые два числа различались хотя бы на 4.
а) Сколько чисел выберет Вася?
б) Сколько способов у Васи сделать это?

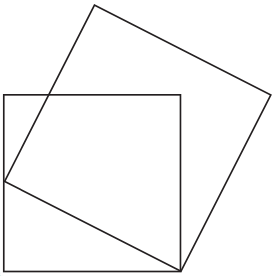
Задача 4. (Михаил Евдокимов)
Два квадрата лежат на плоскости так, как показано на рисунке. Докажите, что центр одного квадрата лежит на диагонали другого.

Задача 5. (Юрий и Сергей Маркеловы)
Квантик загадал целое число от 0 до 99, а Ноутик его отгадывает. Число считается отгаданным, если Ноутик его назвал. За ход Ноутик называет четыре целых числа от 0 до 99, обладающих одним из двух свойств: либо первый разряд у всех чисел совпадает, а вторые разряды последовательные, либо второй разряд у всех чисел совпадает, а первые разряды последовательные (у однозначных чисел первый разряд считаем равным 0). Например, наборы 13, 14, 15, 16 и 3, 13, 23, 33 подходят, а набор 18, 19, 20, 21 – нет. За какое минимальное число ходов Ноутик может гарантированно отгадать число?


