Математический конкурс 2021/22 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (Сергей Полозков)
Можно ли раскрасить каждое ребро куба в один из четырёх цветов так, чтобы все рёбра каждой грани были разного цвета?

Задача 57. (Никита Солодовников)
Непоседливый кладовщик всю неделю переставлял товары по-разному: по алфавиту названий от А до Я и от Я до А, по возрастанию и по убыванию массы, по возрастанию и по убыванию суммы измерений, по возрастанию даты поступления, и каждый раз расположение товаров отличалось от предыдущих. Какое наименьшее количество товаров у него могло быть?

Задача 58. (Татьяна Корчемкина)
У Яны день рождения в январе, а у Ани — в апреле. В 2018 году дни рождения девочек пришлись на вторники. В каком году у обеих девочек день рождения будет во вторник в следующий раз?

Задача 59. (Александр Перепечко)
На фуршете встретились 10 минераловедов. Каждый принёс с собой коллекцию минералов, причём все камни на фуршете оказались разных размеров. За время фуршета каждые два гостя один раз побеседовали друг с другом наедине, обменявшись при этом самыми маленькими камнями, которые у них были на руках в тот момент. Могло ли оказаться, что всего в обменах участвовало:
а) менее 10 камней;
б) хотя бы 60 камней?

Задача 60. (проект Euclidea)
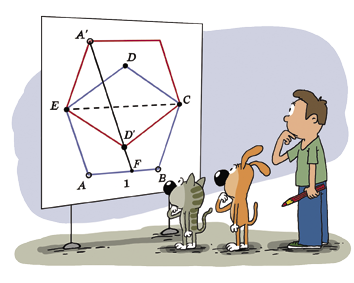
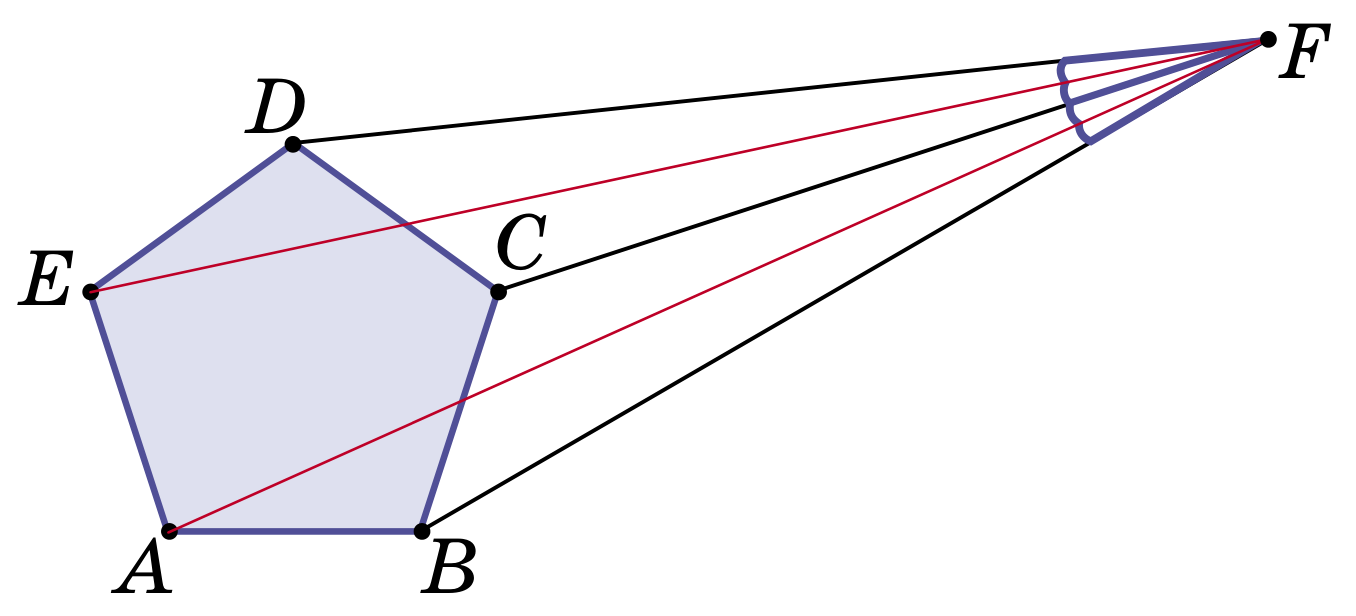
Два одинаковых правильных пятиугольника симметричны относительно пунктирной диагонали (см. рисунок). Найдите длину A’F, если стороны пятиугольников все равны 1.
XI тур
Задача 51. (Борис Френкин)
Из пунктов А и Б навстречу друг другу одновременно выехали с постоянными скоростями велосипедисты Алёша и Боря. В момент их встречи автомобилист Андрей выехал из пункта А в пункт Б. В момент встречи Андрея с Борей Алёша доехал до пункта Б. Кто ехал быстрее — Алёша или Боря?

Задача 52. (Дмитрий Калинин)
У Квантика была пустая, закрытая со всех сторон картонная кубическая коробка. Он разрезал каждую из шести граней этой коробки по какой-то из диагоналей. Могла ли коробка после этого не развалиться на отдельные части?

Задача 53. (Савва Морозкин, 4 класс, Давыдовская гимназия)
Найдите какие-нибудь 12 натуральных чисел (не обязательно различных), произведение которых равно их сумме.

Задача 54. (Максим Прасолов)
В воздухе неподвижно висит кубик. Второй такой же кубик прикладывают к неподвижному так, чтобы какие-то две их квадратные грани в точности наложились друг на друга. Далее второй кубик перекатывают через любое общее ребро кубиков до нового соприкосновения по квадратной грани. После нескольких таких перекатываний второй кубик вернулся в исходное положение. Докажите, что он коснётся первого кубика той же самой гранью, что и вначале.

Задача 55. (Александр Перепечко)
В волшебном кошельке лежат N золотых монет. Квантик знает это и за ход добавляет в кошелёк монету или забирает из него монету себе. После каждого хода Квантика число монет в кошельке уменьшается в два раза, если оно было чётным, а иначе утраивается. При любом ли N Квантик сможет на каком-то ходу опустошить кошелёк, если исходно у Квантика
а) сколько угодно монет;
б) совсем нет монет?

X тур
Задача 46. (Максим Прасолов)
Два посёлка Телегино и Санкино разделены широкой рекой. В Телегино есть магазин, в который зимой ходят жители обоих посёлков, а летом, когда река оттаивает, – только телегинцы. Летом телегинцы стали тратить в магазине в 3 раза больше, чем зимой, но суммарная выручка магазина сократилась в 3 раза. Кто тратил зимой в магазине больше и во сколько раз — телегинцы или санкинцы?

Задача 47. (Константин Кноп)
Даны 9 квадратных карточек с числами 1, 2, …, 9, одинаковые с обратной стороны. Костя выложил их в виде креста, обратной стороной вверх, и сказал Квантику только, что в строке креста числа идут по возрастанию или по убыванию, и в столбце — тоже по возрастанию или по убыванию. За ход Квантик указывает на любую из карточек, а Костя отвечает, какое там число.
а) За какое наименьшее число ходов можно узнать, где лежит карточка 5?
б) Могло ли так случиться, что Квантик задал Косте всего два вопроса и по ответам понял про все 9 карточек, где какая лежит?

Задача 48. (Сергей Губанов)
В ряд стоят 36 человек, среди которых 15 лжецов (всегда лгут), а остальные рыцари (всегда говорят правду). У всех, начиная со второго, спросили про каждого из предыдущих, лжец ли он. (Например, пятому задали четыре вопроса: про первого, второго, третьего и четвёртого.) Докажите, что ответов «Да» и «Нет» было поровну.

Задача 49. (Егор Бакаев)
Вершины двух квадратов соединили двумя отрезками, как на рисунке. Оказалось, что эти отрезки равны. Найдите угол между ними.

Задача 50. (Татьяна Казицына)
Федя вырезал из бумаги несколько клетчатых фигурок. Он заметил, что может сложить все свои фигурки (возможно, с наложением) так, чтобы получилась цифра 0. Аналогично все фигурки можно сложить так, чтобы получалась любая другая цифра (изображения цифр приведены на рисунке). Какое наименьшее число фигурок мог вырезать Федя?


IX тур
Задача 41. (Михаил Евдокимов)
Есть бракованная шахматная доска 8×8 с неправильной раскраской (см. рисунок). Можно ли разрезать её на две части и склеить из них доску с правильной шахматной раскраской (соседние по стороне клетки должны быть окрашены в разный цвет)?


Задача 42. (Михаил Евдокимов)
На экране компьютера горит число 2022. Существует ли такое натуральное число N, что сколько бы раз ни вставить его в середину между цифрами 0 и 2, число на экране компьютера всегда будет делиться на 2022?

Задача 43. (Александр Грибалко)
а) В каждой клетке квадрата 3×3 лежит монета. Некоторые монеты фальшивые (весят одинаково, но легче настоящих), остальные — настоящие (тоже весят одинаково). Известно, что фальшивые монеты занимают целиком либо строку, либо столбец, либо диагональ. Как за одно взвешивание на чашечных весах без гирь найти хоть одну фальшивую монету?
б) Решите ту же задачу для квадрата 9×9, если разрешено сделать два взвешивания.

Задача 44. (Борис Френкин)
Десять раков-отшельников живут в раковинах. Все раки разного размера, и чем больше рак — тем больше его раковина. Раки растут с одинаковой скоростью и хотят менять раковины на более просторные. Если они нашли пустую раковину, её забирает самый большой рак из тех, у кого раковина меньше этой (если такой рак найдётся). В его прежнюю раковину селится следующий (меньший) по размеру, в раковину этого рака — следующий по размеру и т.д. Оставшаяся раковина выбрасывается.
Через некоторое время не осталось ни одной раковины из первоначальных. Обязательно ли каждая имеющаяся раковина больше каждой из первоначальных?

Задача 45. (Михаил Евдокимов)
В выпуклом восьмиугольнике ABCDEFGH все углы равны. Внутри него выбрали произвольную точку O. Докажите, что сумма расстояний от точки O до прямых, содержащих стороны восьмиугольника, не зависит от выбора точки O.

VIII тур
Задача 36. (Михаил Фрайман)
У почтальона есть пачка конвертов, из которой ему нужно взять ровно 50 штук. Пока он стоял и методично отсчитывал по одному конверту, к нему подошёл сын-пятиклассник и сказал: «Если бы ты знал, сколько конвертов во всей пачке, то справился бы в два раза быстрее!» Что имел в виду сын и сколько конвертов во всей пачке?

Задача 37. (Александр Грибалко)
Есть четыре различные пентаминошки (пятиклеточные фигурки). Известно, что как ни разбивай их на пары, пентаминошки в каждой паре можно сложить так, что получатся две одинаковые фигуры. Приведите пример, как такое может быть.

Задача 38. (Михаил Евдокимов)
Робот Квантик переставил числа в строке 1, 2, 3, …, 100 так, чтобы получился «алфавитный порядок», то есть сначала идут числа, начинающиеся с 1, затем начинающиеся с 2, и т.д. (числа, начинающиеся с одной цифры, упорядочиваются по второй цифре). Получилась строка: 1, 10, 100, 11, 12, … Сколько чисел осталось на своём месте?

Задача 39. (Фёдор Нилов)
Покрасьте некоторые клетки белого квадрата 5×5 в синий цвет так, чтобы во всех 16 квадратах 2×2 раскраски были различны (не совмещались бы сдвигом).

Задача 40. (Александр Перепечко)
Через точку внутри равностороннего треугольника провели прямые, параллельные сторонам, и измерили площади полученных шести частей треугольника. Могло ли оказаться, что они принимают ровно три различных значения?

VII тур
Задача 31. (Татьяна Корчёмкина)
В этом году в феврале встретилась дата-палиндром: 22.02.2022 (цифры слева направо идут в том же порядке, что и справа налево). Найдите следующую ближайшую дату-палиндром (и докажите, что она действительно ближайшая).

Задача 32. (Александр Перепечко)
а) Нарисуйте на клетчатой бумаге выпуклый шестиугольник, вершины которого лежат в вершинах клеток, а стороны идут не обязательно по сторонам клеток, который можно двумя прямыми разрезать на четыре равные части. (Не забудьте указать разрезы.)
б) Решите ту же задачу для выпуклого семиугольника.

Задача 33. (Борис Френкин)
В турнире по теннису участвовало N теннисистов, каждый сыграл с каждым один матч. В итоге оказалось, что все выиграли поровну матчей (ничьих в теннисе не бывает). В следующем году теннисистов стало на одного больше, и снова каждый сыграл с каждым один матч. Могло ли и теперь оказаться, что все выиграли поровну матчей?

Задача 34. (Максим Прасолов)
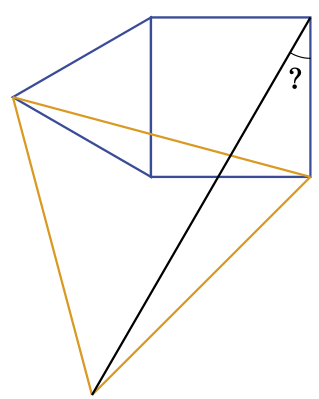
Квадрат и два равносторонних треугольника расположены так, как на рисунке. Найдите угол, отмеченный знаком вопроса.

Задача 35.
У Квантика есть белая клетчатая полоска размером 1×33 клеток. Квантик окунул полоску левым концом в чёрную краску, и несколько первых клеток (не менее одной, но и не все 33) стали чёрными, а остальные остались белыми. Ноутик не видит полоску, но может за один вопрос узнать цвет любой клетки (назвав, какая она по счёту слева). Как ему за 5 вопросов узнать номер самой правой чёрной клетки?

VI тур
Задача 26. (Михаил Фрайман)
Мудрецам A и B выдали по натуральному числу и сказали, что эти числа различаются на 1. «Я не знаю, знаешь ли ты моё число», сказал A, обращаясь к B. Какое число у A?

Задача 27. (Сергей Костин)
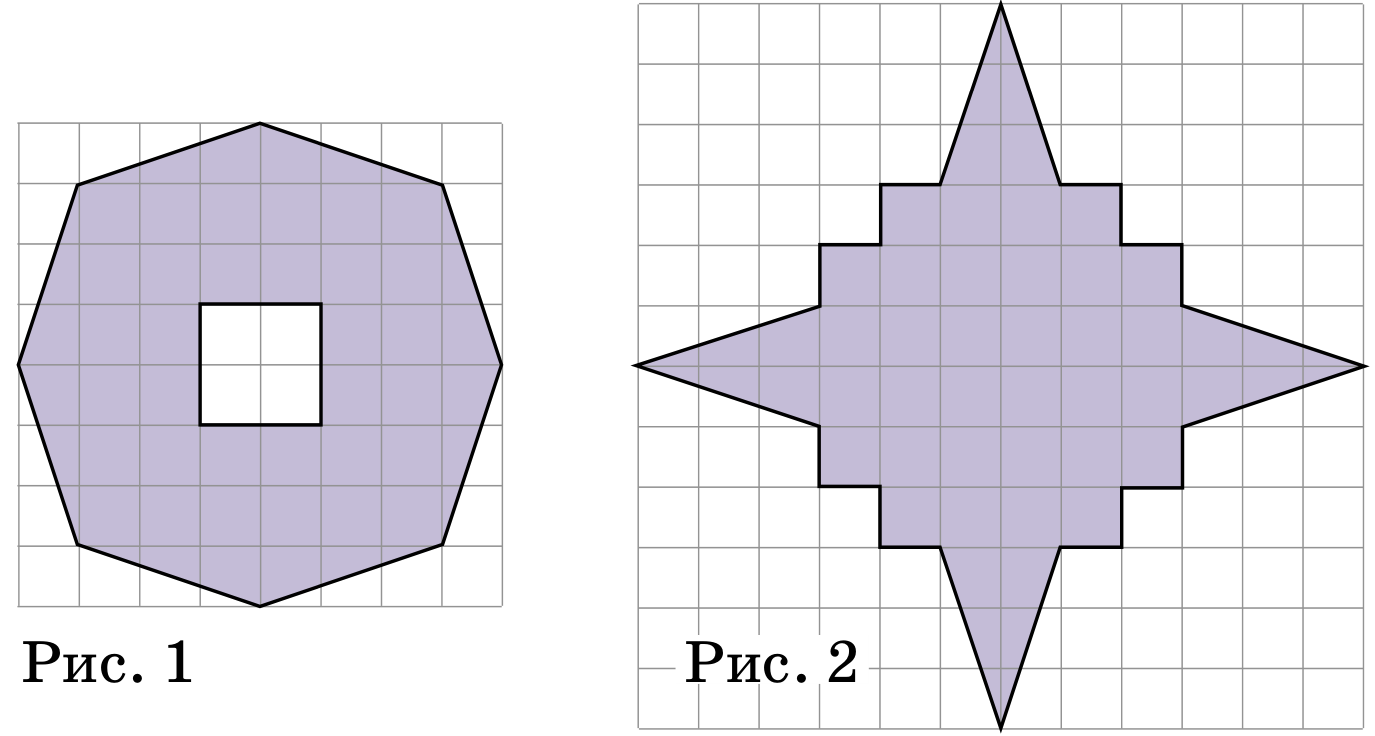
Разрежьте кольцо с дырочкой (рис. 1) на четыре равные части и из полученных частей сложите снежинку (рис. 2).

Задача 28. (Игорь Акулич)
В IV туре нашего конкурса требовалось расшифровать ребус ТУК×5 = СТУК, он имеет два решения. а) Замените пятёрку другой цифрой так, чтобы получился ребус, имеющий решение. б) Докажите, что такая цифра ровно одна. в) Докажите, что решение у нового ребуса единственное.
(Как обычно, одинаковые буквы обозначают одинаковые цифры, разные буквы – разные цифры, и ни одно число не начинается с нуля.)

Задача 29. (Борис Френкин)
Некоторые клетки белой прямоугольной таблицы закрасили синим. Во всех строках количество синих клеток различно, и во всех столбцах тоже. Докажите, что если в таблице не поровну строк и столбцов, то в ней поровну белых и синих клеток.

Задача 30. (Людмила Смирнова)
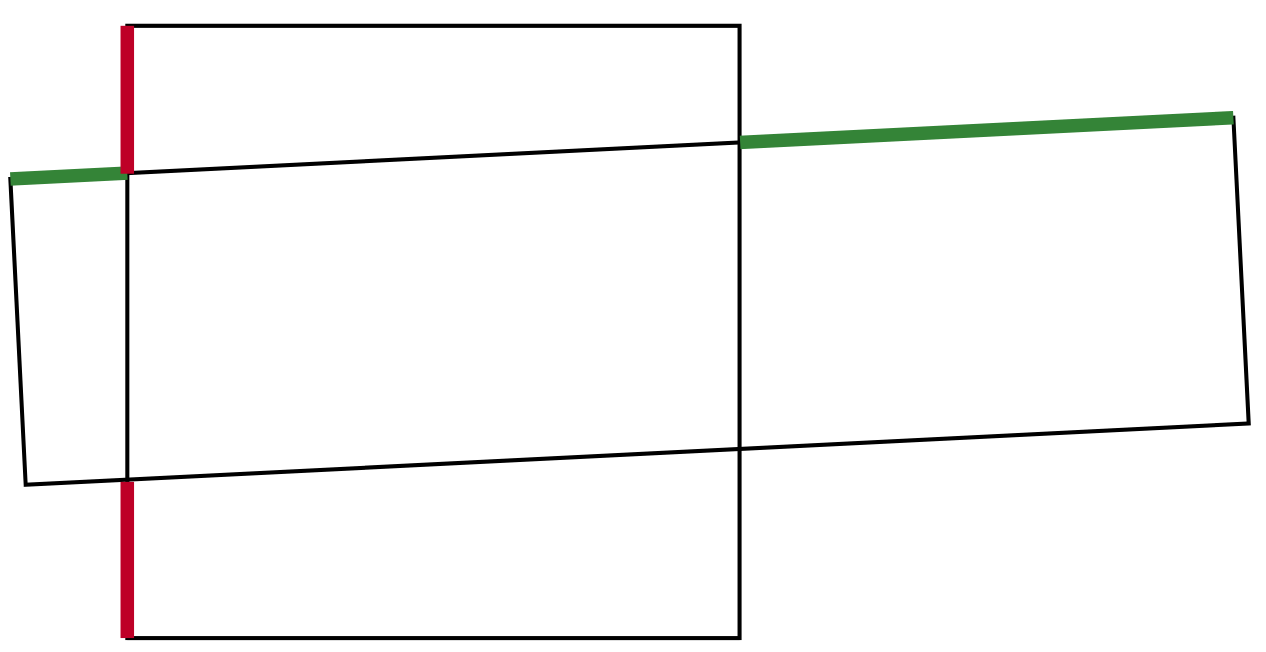
Квадрат 6×6 и прямоугольник 3×12 пересекаются, как показано на рисунке. Докажите, что сумма зелёных отрезков в два раза больше суммы красных отрезков.

V тур
Задача 21. (Борис Френкин)
На острове живут правдолюбы, лжецы и хитрецы (которые могут и сказать правду, и солгать). Всем задали вопрос: «Ты хитрец?» Утвердительно ответили ровно 20 человек. После этого всех спросили: «Ты лжец?» На этот раз сказал «да» ровно 21 человек. Кого на острове больше - хитрецов или лжецов?

Задача 22.
И круг, и прямоугольник легко разрезать на любое количество одинаковых частей. Существует ли фигура с тем же свойством, у которой нет ни центра симметрии, ни оси симметрии? (Части должны быть равны и по форме, и по площади.)

Задача 23. (Игорь Акулич)
Последовательностью Фибоначчи называется последовательность чисел, в которой первые два числа равны 1, а каждое последующее число равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, … Можно ли первые 2022 числа последовательности Фибоначчи разделить на две группы, содержащие поровну чисел, чтобы суммы чисел в этих группах были равны между собой?

Задача 24. (Николай Авилов)
а) Можно ли в белом клетчатом квадрате 10×10 закрасить чёрным несколько клеток так, чтобы число бело-белых соседних клеток равнялось числу бело-чёрных соседних клеток и равнялось числу чёрно-чёрных соседних клеток? (Соседними считаются клетки с общей стороной.)
б) Тот же вопрос про квадрат 9×9.

Задача 25. (Константин Кноп)
Точка F снаружи правильного пятиугольника ABCDE такова, что отрезки ED, EC, AC и AB видны из F под одним и тем же углом (см. рисунок). Под каким? (Говорят, что отрезок MN виден из точки X под углом α, если угол MXN равен α).

IV тур
Задача 16. (Алексей Заславский)
На острове каждый житель либо рыцарь (всегда говорит правду), либо лжец (всегда лжёт). Житель A рассказал такую историю:
- Встретил я жителей B и C. Первый говорит: «Мы оба лжецы». А второй кивает: «Это правда».
Про кого из A, B, C можно однозначно определить, кто он - рыцарь или лжец?

Задача 17. (Назар Агаханов)
Расшифруйте ребус:
ТУК + ТУК + ТУК + ТУК + ТУК = СТУК.
(Найдите все ответы и докажите, что других нет. Одинаковыми буквами обозначены одинаковые цифры, разными - разные, и ни одно число не начинается с ноля.)

Задача 18. (Сергей Дворянинов)
Когда Робинзон Крузо попал на необитаемый остров, у него было 200 ружейных зарядов. Ради их экономии он решил каждый день тратить на охоте не более 5% имеющихся на то утро зарядов. В какой-то момент Робинзон уже не мог делать выстрелы, придерживаясь своего правила. Сколько патронов он истратил к этому моменту?

Задача 19. (Михаил Евдокимов)
При каких N большой клетчатый уголок, состоящий из трёх квадратов N×N, можно разрезать по линиям сетки на обычные трёхклеточные уголки?

Задача 20. (Михаил Евдокимов)
а) Маша испекла торт, имеющий форму квадрата со стороной 21 см. Затем она выбрала внутреннюю точку на одной из сторон и сделала надрез длиной 20 см из этой точки перпендикулярно выбранной стороне. В итоге Маша сделала так для каждой из 4 сторон. Обязательно ли при этом был отрезан хотя бы один кусок?
б) Решите ту же задачу, если Маша испекла торт в форме правильного шестиугольника диаметра 35 см и сделала от каждой стороны разрез длиной 20 см перпендикулярно этой стороне.

III тур
Задача 11. (Максим Дидин)
Барон Мюнхгаузен утверждает, что записал дробь A/B, где A и B - различные натуральные числа, а потом вычеркнул какую-то цифру в числителе и какую-то - в знаменателе так, что получившаяся дробь стала равна дроби B/A. Могло ли такое быть?.

Задача 12. (Егор Бакаев)
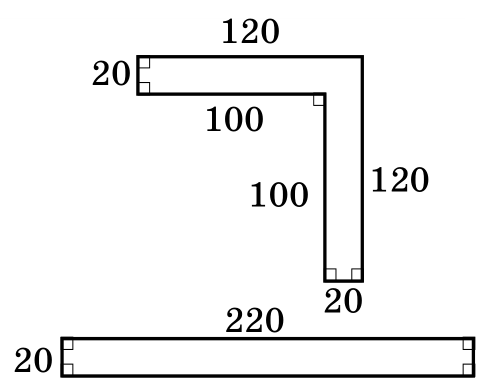
Квантик и Ноутик выгуливают своих собак не далее чем в 100 м от своих домов (то есть в таких точках, расстояние от которых до ближайшей точки дома не превышает 100 м). Они живут в домах, формы и размеры которых указаны на рисунке. Дома расположены далеко друг от друга и от других домов, и вокруг них нет ничего, мешающего прогулке. У кого больше площадь территории, на которой он выгуливает свою собаку?

Задача 13. (Борис Френкин)
В таблице 10×10 половина клеток красные, половина - синие. Назовём строку или столбец чистыми, если в них все клетки одного цвета. Какое наибольшее суммарное число чистых строк и столбцов может быть в такой таблице и почему?

Задача 14. (Михаил Евдокимов)
На картинке вы видите часть большой решётки, составленной из шестиугольников, у которых все стороны равны и углы тоже. Все вершины шестиугольников раскрасили, каждую - в чёрный или белый цвет. Докажите, что найдутся три одноцветные вершины, образующие равносторонний треугольник.


Задача 15. (Илья Сиротовский)
Петя записывает 9-значные числа. На первое место (самое левое) он пишет любую цифру от 1 до 9, на второе место - от 1 до 8, на третье - от 1 до 7, …, на девятое (самое правое) - цифру 1. Сколько чисел, делящихся на 7, может получить Петя?

II тур
Задача 6. (Максим Волчкевич)
Кресла в самолёте расположены в 30 рядов. Расстояние между рядами одно и то же, расстояние между спинками кресел, идущих друг за другом, равно 80 см. С целью добавить новые ряды, пустое пространство перед каждым креслом решили уменьшить на 5 см. Сколько теперь поместится рядов в салоне самолёта?

Задача 7. (Константин Кноп)
Во внешнюю сторону от квадрата построены два равносторонних треугольника с вдвое меньшей стороной (см. рисунок). Чему равен угол, отмеченный знаком вопроса?

Задача 8. (Александр Перепечко)
Несколько интровертов и экстравертов хотят разбиться на четыре команды. Каждый по очереди выбирает команду, причём интроверты выбирают какую-то команду минимального размера на момент выбора, а экстраверты – максимального. Могли ли команды получиться попарно различного размера?

Задача 9. (Алексей Толпыго)
Дан правильный шестиугольник ABCDEF. Любые три его вершины образуют треугольник, всего таких треугольников 20. Квантик хочет отметить внутри шестиугольника как можно меньше точек, чтобы внутрь каждого из этих 20 треугольников попала хоть одна отмеченная точка. Приведите пример, как отметить точки, чтобы выполнялось это условие, и докажите, что меньше точек отметить нельзя.

Задача 10. (Александр Перепечко)
В классе в турнире по армрестлингу каждый сыграл с каждым (ничьих в армрестлинге не бывает). Каждый мальчик одержал вдвое больше побед, чем потерпел поражений, а каждая девочка – вдвое меньше побед, чем поражений.
а) Приведите пример, как такое могло быть.
б) Обязательно ли при этом какая-нибудь девочка победила какого-нибудь мальчика?

I тур
Задача 1. (Сергей Шашков)
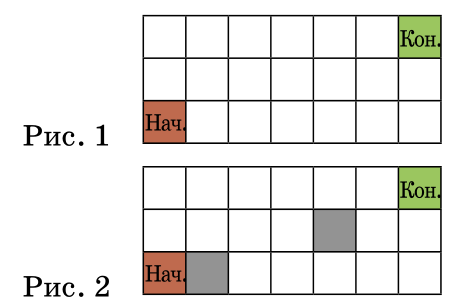
На склад, пол которого имеет вид прямоугольника 3×7 клеток, привезли кубический холодильник, он занимает одну клетку. Холодильник можно перекатывать через ребро, ставя на бок, но нельзя переворачивать вверх ногами. Нарисуйте пример пути, по которому можно перекатить холодильник из нижней левой клетки в правую верхнюю, чтобы и в начале, и в конце он стоял дном вниз, если изначально
а) склад пустой (рис. 1);
б) на складе уже заняты две клетки (рис. 2).

Задача 2. (Татьяна Корчемкина)
Полина, Лена и Ирина впервые пришли на кружок и решили познакомиться.
– Меня зовут Лена, – сказала одна из них.
– А меня зовут Ирина, – сказала вторая.
Третья девочка промолчала.
Известно, что Полина всегда говорит правду, Лена всегда лжёт, а Ирина иногда говорит правду, а иногда – неправду. Как на самом деле зовут каждую из девочек?

Задача 3. (Кирилл Банков)
а) Можно ли разрезать какой-нибудь прямоугольник на несколько равнобедренных прямоугольных треугольников, среди которых нет одинаковых?
б) Можно ли так разрезать квадрат?

Задача 4. (Сергей Костин)
Расставьте в клетках квадрата 3×3 различные натуральные числа, в записи каждого из которых могут присутствовать лишь цифры 1 и 2, так чтобы сумма чисел в каждой строке и в каждом столбце была одна и та же.

Задача 5. (Александр Перепечко)
Есть проволочный каркас прямоугольного ящика и верёвка. Разрешается выбрать любые несколько точек на каркасе, соединить их подряд натянутой верёвкой и измерить её длину, от первой точки до последней. Предложите способ за два таких измерения найти суммарную площадь всех шести граней ящика.


