Математический конкурс 2022/23 учебного года
Конкурс окончен! Поздравляем победителей!
XII тур
Задача 56. (Татьяна Корчемкина)
Вася решил разнообразить свой досуг. Каждое утро он смотрит в календарь. Если сегодняшнее число делится на 2, то в этот день Вася читает книги, если делится на 3 – решает задачи, а если делится на 4 – играет в футбол. Но делать все три дела в один день у Васи не получается – в такие дни он выбирает любые два занятия из трёх. В результате за август Вася играл в футбол 5 раз. А сколько раз он читал книги и сколько раз решал задачи?

Задача 57. (Татьяна Голенищева-Кутузова)
Можно ли разрезать прямоугольник 3×4 клетки на а) четыре; б) пять клетчатых прямоугольников, среди которых нет одинаковых?

Задача 58. (Татьяна Казицына и Борис Френкин)
В каждой клетке доски 8×8 стоит единица или минус единица. В каждом кресте, состоящем из строки и столбца, произведение всех 15 чисел равно числу, стоящему на их пересечении. Может ли произведение всех чисел на доске равняться минус единице?

Задача 59. (Александр Перепечко)
У Квантика есть 11 шестерёнок диаметра 10, 11, 12, …, 20 см. Он хочет соединить их все последовательно в каком-то порядке, и к первой шестерёнке присоединить моторчик, который будет вращать её со скоростью 1 оборот в минуту. Какая наибольшая достижимая скорость вращения последней шестерёнки? (Также укажите какой-то порядок расположения шестерёнок, при котором эта скорость достигается, и докажите, что она действительно наибольшая возможная.)

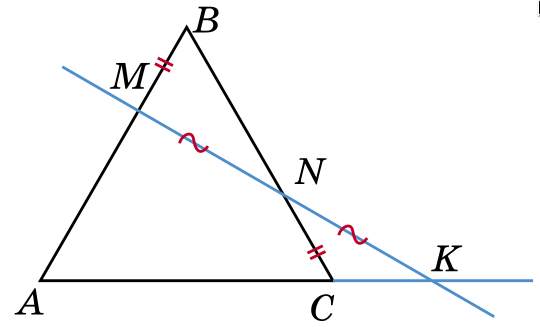
Задача 60. (Роман Хазанкин)
Прямая пересекает стороны AB, BC и продолжение стороны AC равностороннего треугольника ABC в точках M, N и K соответственно (см. рисунок). Оказалось, что MB = NC и MN = NK. Докажите, что прямые MN и AB перпендикулярны.

XI тур
Задача 51. (Егор Бакаев)
Представьте число 2023 как сумму девяти чисел, каждое из которых состоит только из цифр 7.

Задача 52. (Игорь Акулич)
Квадрат N×N разбит на клетки 1×1. Изначально все они белые. Каждую минуту, пока это возможно, Квантик выбирает белую клетку, с которой соседствует по стороне чётное число чёрных клеток (0, 2 или 4) и красит её в чёрный цвет. Какое наибольшее количество клеток квадрата может закрасить Квантик?

Задача 53. (Борис Френкин)
Петя написал на доске строчку из натуральных чисел. Каждое следующее больше предыдущего. Начиная с третьего, каждое число равно сумме двух предыдущих. Вася стёр первое число. Среди оставшихся чисел есть 100. Есть ли среди них 600?

Задача 54. (Георгий Караваев)
Боб решил отправить Алисе несколько бобров. Оказавшись на почте, Боб обнаружил, что не помнит, сколько бобров он положил в каждую из четырёх коробок. К счастью, на почте нашёлся старенький боброметр — устройство, позволяющее узнать суммарное количество бобров в коробках, помещённых в него. Однако его гарантийный срок давно истёк, и поэтому боброметр при измерениях может ошибаться, но не более чем на 17 бобров. Боб по очереди загрузил всевозможные пары коробок в боброметр и получил такие результаты: 43, 99, 123, 141, 233, 255. Сколько всего бобров Боб хотел отправить Алисе?

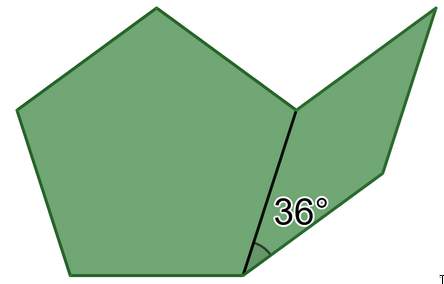
Задача 55.
К стороне правильного пятиугольника приставили ромб с углом 36°, как показано на рисунке. Разделите получившийся семиугольник на три равные (по форме и размерам) части.

X тур
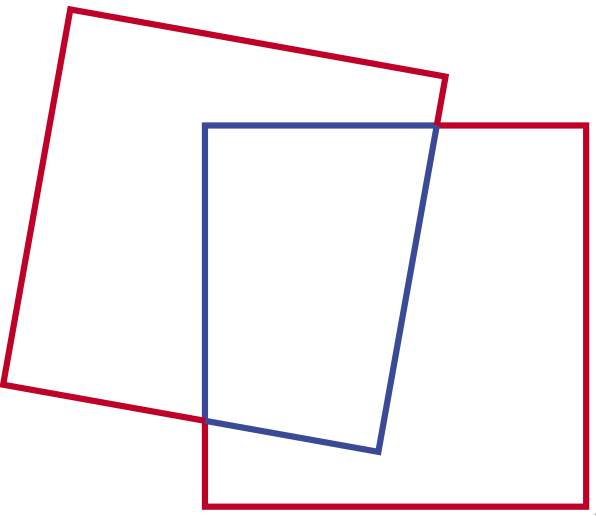
Задача 46. (Георгий Караваев)
Квантик положил два одинаковых квадрата на стол так, что они налегают друг на друга, но не совпадают. Затем он обвёл красным карандашом получившуюся фигуру, а оставшиеся части сторон квадратов обвёл синим карандашом. Оказалось, что периметр красной фигуры в полтора раза больше периметра синей. Во сколько раз периметр красной фигуры больше периметра одного квадрата?

Задача 47. (Михаил Евдокимов)
Барон Мюнхгаузен утверждает, что можно выписать на доску в некотором порядке 9 различных цифр и поставить между некоторыми из них знак «+» так, чтобы результат был равен 2023. Не ошибается ли барон?

Задача 48. (Марина Хачатурян)
В белом клетчатом листочке 10×10 одну клетку закрасили красным. Затем листочек сложили несколько раз по линиям сетки и диагоналям клеток, проткнули иголкой и развернули. Могло ли случиться, что внутри каждой белой клетки, не на сгибах, есть точка прокола, а внутри красной клетки прокола нет?

Задача 49. (Сергей Полозков)
Емеля перемещается только на печи, которая ездит на дровах — полено на километр — и вмещает 60 поленьев. Вчера Емеля выехал на печи из дома, на некотором расстоянии от него сделал склад поленьев, после чего вернулся обратно. Сегодня Емеля снова набрал поленьев, выехал из дома, проехал через склад… и не вернулся — кончились поленья. Как далеко от дома он мог оказаться? Найдите наибольшее возможное расстояние.

Задача 50. (Георгий Караваев)
Круг разделили двумя перпендикулярными хордами на 4 части. Могли ли их площади равняться 2022, 2023, 2024 и 2025 см²?

IX тур
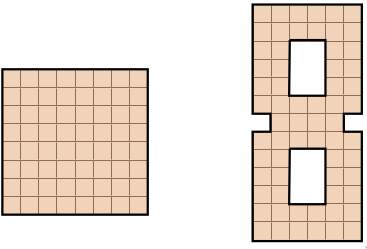
Задача 41. (Сергей Костин)
Пьеро решил поздравить с 8 Марта Мальвину, и кроме новой песни сочинил для неё задачу: разрезать квадрат 8 × 8 (слева) на четыре (не обязательно одинаковые) части и сложить из этих частей фигуру в виде цифры 8 (справа). Мальвине помог решить эту задачу Буратино. А справитесь ли вы с задачей Пьеро?

Задача 42. (Егор Бакаев)
В один из дней этого года Квантик, взглянув на календарь, взял факториал от текущего числа и получил число минут в текущем месяце. В какую дату это было? (Факториал числа n — это произведение чисел от 1 до n, обозначается n!. Например, 4! = 1•2•3•4 = 24.)

Задача 43. (Михаил Евдокимов)
Три одинаковых равнобедренных треугольника с основанием 1 расположены в квадрате так, как показано на рисунке (все вершины лежат на сторонах квадрата, на нижней стороне у соседних треугольников есть общая вершина). Чему равна сторона квадрата, если его центр лежит на одной из сторон третьего треугольника? Найдите все возможные варианты.

Задача 44. (Алексей Заславский)
В полдень Петя поехал на велосипеде из деревни А в деревню Б, а Вася из Б в А. Каждый из них ехал с постоянной скоростью до момента встречи. Встретившись, они остановились на 10 минут, чтобы поговорить. Потом один из них увеличил скорость на 28%, а другой на 40%. В результате каждый приехал в другую деревню в такое же время, как если бы ехал весь путь без остановки с начальной скоростью. Во сколько произошла встреча?

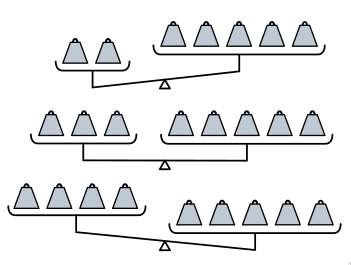
Задача 45. (Георгий Караваев)
У Даши есть грузы двух видов, разных по весу и отличающихся лишь цветом. Она сделала несколько чёрно-белых фотографий взвешиваний с этими грузами. Можно ли определить, во сколько раз отличаются веса грузов разных видов?

VIII тур
Задача 36. (Леонид Петров)
У профессора есть несколько будильников. Вечером он заводит все будильники с интервалами в 5 минут: на 7:00, 7:05, 7:10 и так далее. Когда будильник звонит, профессор мгновенно нажимает кнопку «отложить», а будильник переносит звонок на 9 минут вперёд. Профессор окончательно просыпается, когда одновременно звонят сразу 4 будильника. Успеет ли он проснуться ранее 9:30 утра, чтобы успеть на свою зум-лекцию?

Задача 37. (Сергей Токарев)
Из деревянного бруса в форме параллелепипеда 1 дм × 1 дм × 50 дм несколькими поперечными распилами получили бруски, из которых склеили каркас куба. Какова высота этого каркаса, если его рёбра в поперечном сечении имеют размер 1 дм × 1 дм?

Задача 38. (Михаил Евдокимов)
Фокусник хочет заготовить 10 карточек, написать на каждой натуральное число, не большее 90, чтобы все числа были различны, и показывать такой фокус: зритель наугад выбирает две карточки, называет фокуснику сумму чисел на них, а фокусник тут же отгадывает, какие две карточки у зрителя. Помогите фокуснику найти числа и объясните, почему фокус будет получаться.

Задача 39. (Дмитрий Калинин, Сергей Костин)
Квадрат 7 × 7 разрезали по границам клеток на 7 прямоугольников одинакового периметра. Обязательно ли все эти прямоугольники одинаковые?

Задача 40. (Егор Бакаев)
Один из углов прямоугольника поделён двумя лучами на три равных угла. Один из этих лучей делит сторону прямоугольника пополам. Второй луч пересекает другую сторону. В каком отношении он её делит?

VII тур
Задача 31. (Егор Бакаев)
В интернет-магазине доставка стоит 500 рублей, но при сумме заказа от 1500 рублей доставка бесплатна. Иван Иванович и Иван Никифорович заказали с доставкой одинаковые зонтики, но Ивану Никифоровичу в честь дня рождения сделали на товар скидку 10%. Каково же было удивление Ивана Никифоровича, когда он заплатил на 340 рублей больше, чем Иван Иванович. Сколько стоил зонтик?

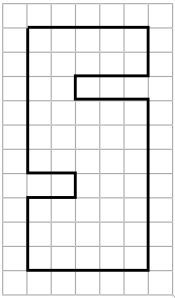
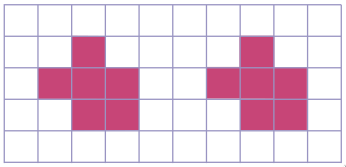
Задача 32. (Татьяна Корчемкина)
Разрежьте «цифру 5» на рисунке по линиям сетки на 9 различных пятиклеточных частей (фигуры, которые можно совместить поворачиванием и переворачиванием, считаются равными).

Задача 33. (Фёдор Нилов)
Можно ли покрасить все натуральные числа в три цвета так, чтобы сумма любых двух чисел разных цветов была бы покрашена в третий цвет?

Задача 34. (Павел Кожевников)
Сколькими способами можно расставить в таблице 3×3 числа 1, 2,…, 9 (каждое по разу) так, чтобы суммы во всех строках и столбцах были нечётные?

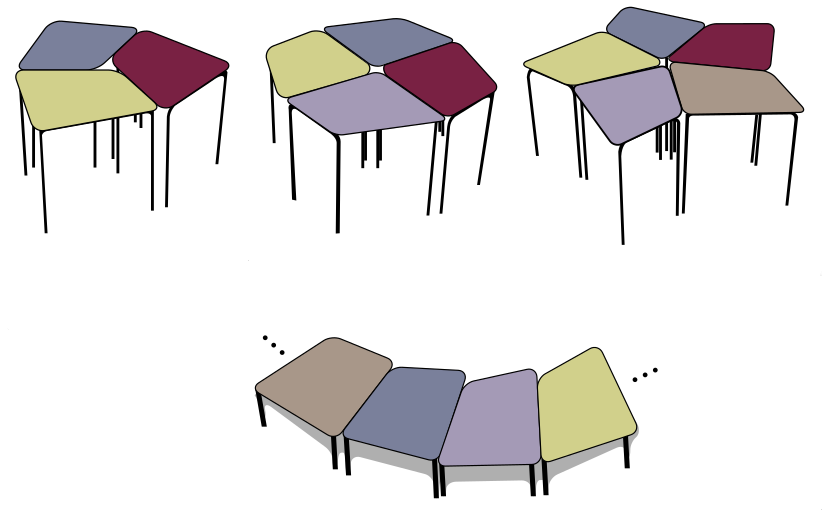
Задача 35. (Егор Бакаев)
В офис привезли много одинаковых четырёхугольных столов, у каждого стола все стороны разной длины. Оказалось, что и 3 таких стола, и 4, и 5 можно поставить по кругу, одинаковыми углами к центру, так чтобы между соседними столами не было зазора.
Сколько таких столов можно поставить по кругу, одинаковыми сторонами наружу и без зазоров между соседними столами? Укажите все варианты и докажите, что других нет.

VI тур
Задача 26. (Татьяна Корчемкина)
На остановке останавливаются автобусы 3, 4 и 5, причём автобус №3 ходит каждые 3 минуты, автобус №4 – каждые 4 минуты, а автобус №5 – каждые 5 минут. Аня заметила, что на остановку приходило по одному автобусу в 10:00, 10:01, 10:02, 10:03 и 10:05. Какой был номер у автобуса, приехавшего в 10:05, и почему?

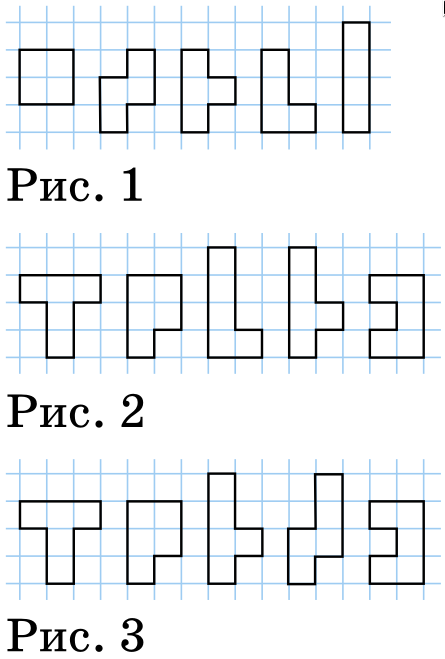
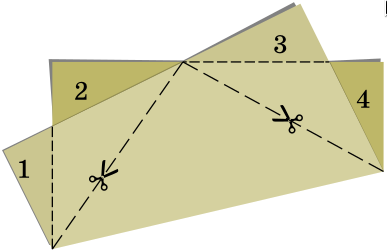
Задача 27. (Татьяна Корчемкина)
Ребятам задали на дом вырезать из картона 5 тетраминошек, как на рисунке 1.
Перед уроком Петя и Вася поняли, что неправильно записали задание и вырезали по пять пентаминошек. Фигурки Пети изображены на рисунке 2, а Васины – на рисунке 3.
Сможет ли Петя отрезать по одной клетке от каждой своей фигурки так, чтобы в результате получился нужный набор? А сможет ли Вася? (нарисуйте, какие клетки нужно отрезать, или объясните, почему получить нужный набор не удастся).

Задача 28. (Олег Смирнов)
Федя увидел в спортивном магазине гантели. Каждая гантель представляла собой два одинаковых стальных диска, насаженных на стержень. У разных гантелей диски были разного диаметра, но толщина всех дисков была одна и та же, и все стержни были одинаковыми. Увидев, что гантели с дисками диаметра 5 см весят 5 кг, а гантели с дисками диаметра 7 см весят 7 кг, Федя удивился: это не сходилось с известной ему формулой πR² для площади круга радиуса R. Разберитесь, что не учёл Федя, и найдите диаметр дисков у гантелей весом 13 кг.

Задача 29. (Борис Френкин)
По шахматной доске 8×8 прошла хромая ладья (каждым ходом она переходила в клетку, соседнюю по стороне; возможно, в некоторые клетки она зашла несколько раз, а в некоторые не зашла совсем). Количество вертикальных ходов было вдвое больше, чем количество горизонтальных. Ладья начала движение в левом нижнем углу, а закончила в каком-то другом. В каком именно?

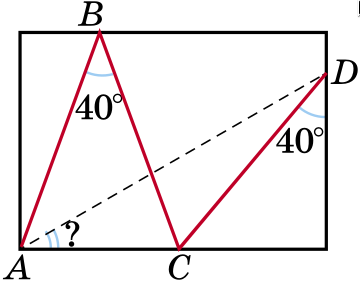
Задача 30. (Михаил Евдокимов)
Вершины ломаной ABCD лежат на сторонах прямоугольника (см. рисунок). Все звенья ломаной равны, а два отмеченных на рисунке угла равны 40°. Чему равен угол CAD?

V тур
Задача 21. (Татьяна Корчемкина)
В поезде нечётное количество вагонов, причём между средним и седьмым по счёту – два вагона. Сколько всего вагонов может быть в этом поезде? Укажите все варианты и докажите, что других нет.

Задача 22. (Татьяна Корчемкина)
Квантик заменил все цифры и знаки арифметических действий в левой части верного равенства буквами (одинаковые символы – одинаковыми буквами, разные символы – разными). Мог ли он получить запись ABCABCA = 2023?

Задача 23. (Александр Толмачев)
Вася сложил квадратный лист бумаги так, как показано на рисунке. Оказалось, что четыре отмеченных треугольника равны. После этого пришёл Петя и сделал разрезы вдоль жирных пунктирных линий, а затем развернул лист и сказал Васе, что у него тоже получился квадрат! Не ошибся ли Петя?

Задача 24. (Сергей Полозков)
Квантик написал на каждой грани куба целое число (все шесть чисел различны). Потом в каждой вершине он написал сумму чисел на трёх содержащих эту вершину гранях. Ноутик выписал полученные восемь сумм в ряд по возрастанию. Могло ли получиться так, что все разности между соседними числами в этом ряду одинаковы?

Задача 25. (Борис Френкин)
На острове в разных местах есть пристань, крепость и деревня. Расстояние по прямой от пристани до крепости равно 3 км, от крепости до деревни – тоже 3 км. Петя получил достоверные сведения, что на острове зарыт клад. Известны расстояния по прямой до клада от пристани, крепости и деревни. Петя нашёл такое место, но не обнаружил ни клада, ни следов предыдущих раскопок. Сколько километров от пристани до деревни?

IV тур
Задача 16. (Татьяна Корчемкина)
В дате последнего дня этого года (31.12.22) одна цифра встречается один раз, другая — два раза, третья — три раза. Найдите следующую дату с тем же свойством.

Задача 17. (фольклор)
Известно, что N — натуральное число, а среди дробей 2/N, 3/N, 4/N, 5/N, 6/N, 7/N, 8/N, 9/N, 10/N ровно одна несократимая. Какая?

Задача 18. (Сергей Полозков)
Квантик вырезал две одинаковые шестиклеточные фигуры, как на рисунке. Можно ли ими обклеить поверхность куба без наложений и пустых мест?

Задача 19. (Татьяна Казицына)
Буквы русского алфавита заменены числами от 1 до 33 в неизвестном порядке (разные буквы — разными числами). Эмма записала этим кодом своё имя (без пробелов), и так же поступили Вера и Леонтий.
а) Может ли быть, что Эмма и Вера написали одно и то же число?
б) Может ли быть, что одно и то же число написали Эмма и Леонтий?

Задача 20.
Найдите наибольшую возможную площадь четырёхугольника, какие-то две стороны которого равны 1 и какие-то две стороны равны 2.

III тур
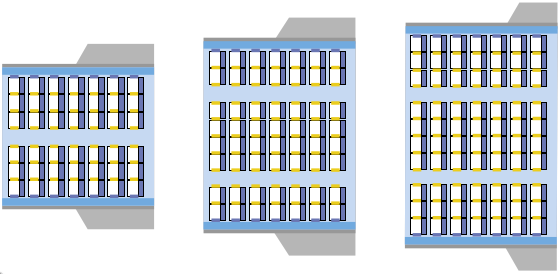
Задача 11. (Сергей Дориченко)
Серёжа считает место в самолёте удобным, если оно у окна или у прохода. Каждый раз место ему выбирает компьютер случайным образом. Самолёты бывают трёх типов, как на рисунке. В самолёте какого типа вероятность попасть на удобное место больше всего? А в каком — меньше всего?

Задача 12. (Сергей Костин)
Барон Мюнхгаузен утверждает, что по его чертежам печь, изображённую на рисунке сверху, разрезали на 10 равных частей и из этих частей сложили печь, изображённую на рисунке снизу. Не ошибается ли барон?

Задача 13. (Борис Френкин)
На блюде лежат пирожки с капустой, картошкой и яблоками: больше всего — с капустой, а меньше всего — с яблоками. Школьники по одному подходят и берут по одному пирожку, причём того сорта, которого в этот момент больше всего, а если такой сорт не один — любого из таких сортов. Вскоре оказалось, что пирожков с яблоками столько, сколько всех остальных, причём все три сорта ещё есть. Можно ли определить, сколько в этот момент на блюде пирожков каждого сорта?

Задача 14. (Александр Толмачев)
Равносторонний треугольник со стороной 3 разбит на 9 равносторонних треугольников со стороной 1 (см. рисунок). Расставьте в них числа от 1 до 9 (по одному числу в треугольник) так, чтобы сумма чисел в любом равностороннем треугольнике со стороной 2 была квадратом целого числа.
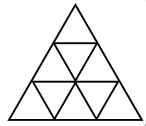

Задача 15. (Николай Авилов)
У Васи сломалась головоломка «Змейка Рубика», состоящая из 24 одинаковых треугольных призм. Каждая призма — это половинка кубика 1×1×1. Из 16 таких полукубиков он склеил 8 различных фигурок так, как на фото. Сможет ли Вася из этих восьми фигурок сложить куб 2×2×2?


II тур
Задача 6. (Борис Френкин)
В гостиной, спальне и кухне висят градусники. В спальне температура всегда выше на 1 градус, чем в гостиной, а на кухне — ещё на 1 градус выше. Петя записал утром, днём и вечером показания всех трёх градусников, но ровно в одном числе сделал опечатку. В результате получились числа (в каком-то порядке): 17, 18, 19, 22, 25, 25, 26, 27, 27. В каком числе опечатка и что должно там стоять? Ответ обоснуйте.

Задача 7. (Татьяна Корчемкина)
Маша сшила восьмиугольную скатерть из пяти квадратов и четырёх равнобедренных прямоугольных треугольников (см. рисунок). А можно ли сшить точно такую же скатерть из одного квадрата и восьми равнобедренных прямоугольных треугольников (не обязательно одинаковых)


Задача 8. (Сергей Костин)
В слове СЛУЧАЙНОСТЬ школьники случайным образом заменяют буквы на цифры (одинаковые буквы на одинаковые цифры, а разные буквы на разные цифры, причем первая буква слова не может заменяться на цифру 0). Найдите вероятность того, что полученное в результате число делится на 3. (То есть какую долю среди всех возможных вариантов составляют числа, делящиеся на 3.)

Задача 9. (Михаил Евдокимов)
Все грани треугольной пирамидки — одинаковые равносторонние треугольники. У каждой грани отметили середины сторон и соединили друг с другом, разбив грань на 4 одинаковых маленьких треугольничка. Каждый из этих 16 получившихся треугольничков окрасили в один из трёх цветов — красный, синий или зелёный, — так, что любые два треугольничка с общей стороной окрашены в разные цвета (не забудьте, что треугольнички с общей стороной могут принадлежать и разным граням). Какое наибольшее количество красных треугольничков могло получиться?

Задача 10. (Сергей Костин)
Существует ли многоугольник, который с помощью одного прямолинейного разреза можно разрезать на треугольники с площадями 1, 2, 3, а с помощью другого прямолинейного разреза — на треугольники с площадями 2, 2, 2?

I тур
Задача 1. (Сергей Дориченко)
На чаепитии всех угощали конфетами. И Петя, и Вася взяли себе по две конфеты каждого вида, но съели только по 10 конфет каждый, а остатки принесли домой. Сколько всего видов конфет было на чаепитии, если Петя принёс домой конфеты только трёх видов, а Вася — шести?

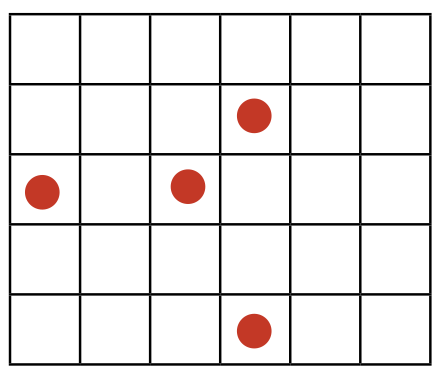
Задача 2. (Михаил Евдокимов)
Малыш и Карлсон делят торт 5×6, украшенный вишенками (см. рисунок). Может ли Карлсон так разрезать торт на две одинаковые по форме и размеру части, что все вишенки достанутся ему?

Задача 3. (Алексей Канель-Белов)
Гарри Поттер поместил в толщу воды неподвижный ледяной кубик со стороной 1 см, после чего вся вода, находящаяся не дальше, чем на 1 см хоть от какой-то точки кубика, тоже замёрзла. Докажите, что получившийся кусок льда можно разрезать на части и сложить из них всех несколько фигур, каждая из которых — кубик, цилиндр или шарик.

Задача 4. (Борис Френкин)
На острове 99 жителей, и каждый — либо спорщик, либо подпевала. Всех по очереди спросили, кого на острове больше — спорщиков или подпевал. Каждый, кроме первого, отвечал так: если он подпевала, повторял ответ предыдущего, а если спорщик — отвечал наоборот. В результате 75 островитян ответили неправильно. Можно ли только по этим данным определить, кого на острове больше: спорщиков или подпевал?

Задача 5. (Фёдор Нилов)
В вершинах куба расставили 8 чисел так, что на любых двух параллельных рёбрах общая сумма чисел одна и та же. Сколько среди этих 8 чисел может быть различных? (Укажите все варианты, сколько различных чисел может быть, и докажите, что других вариантов нет.)


